The horizontal asymptote of a function is a concept that describes the function’s behavior as x approaches positive or negative infinity. It’s represented by a horizontal line that the graph of the function approaches but doesn’t necessarily touch or cross. Understanding horizontal asymptotes is crucial for analyzing the end behavior of functions, especially in calculus and mathematical analysis.
Understanding Horizontal Asymptotes
A horizontal asymptote for a function y = f(x) is defined as a horizontal line y = k if either the limit of f(x) as x approaches infinity (x→∞) or as x approaches negative infinity (x→-∞) equals k. Mathematically, this is expressed as:
lim x→∞ f(x) = k or lim x→-∞ f(x) = k
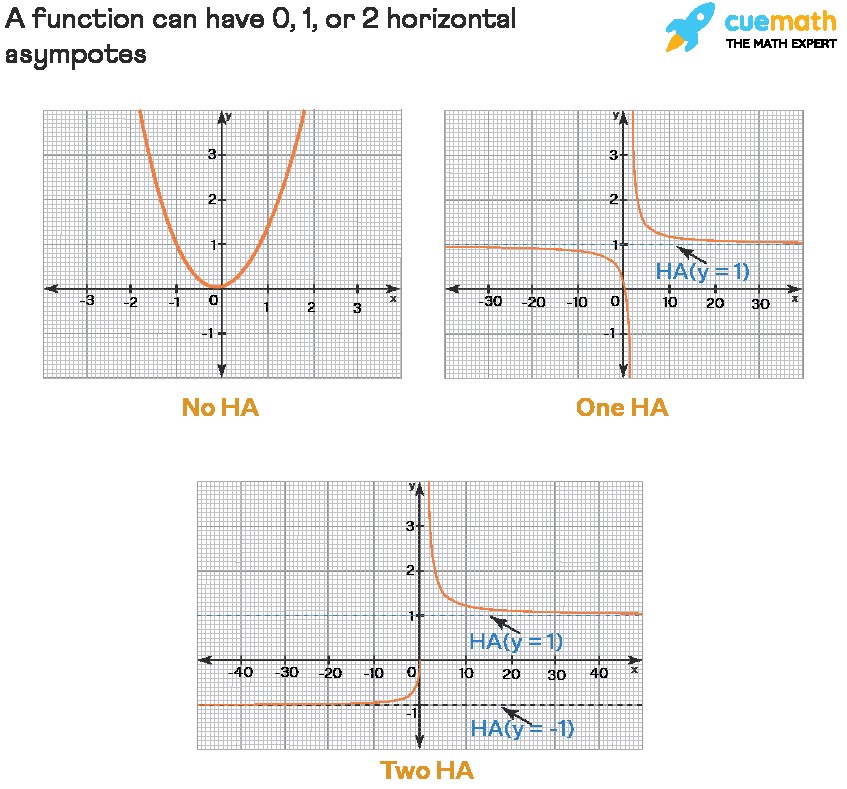
Here, k must be a real number. Essentially, a horizontal asymptote indicates the value that the function approaches as x becomes extremely large (positive or negative). A function can have at most two horizontal asymptotes – one as x approaches positive infinity and another (possibly the same one) as x approaches negative infinity. It’s also possible for a function to have just one or even no horizontal asymptotes at all.
Horizontal asymptotes are visualized as dashed horizontal lines when graphing functions. They are not part of the function’s curve but serve as a guide to illustrate the function’s end behavior. Graphing calculators typically do not display horizontal asymptotes, emphasizing their nature as guiding, imaginary lines rather than components of the graph itself.
Image showing graphs with different horizontal asymptotes, illustrating the concept of a function approaching a horizontal line as x goes to infinity or negative infinity.
Can a Graph Cross a Horizontal Asymptote?
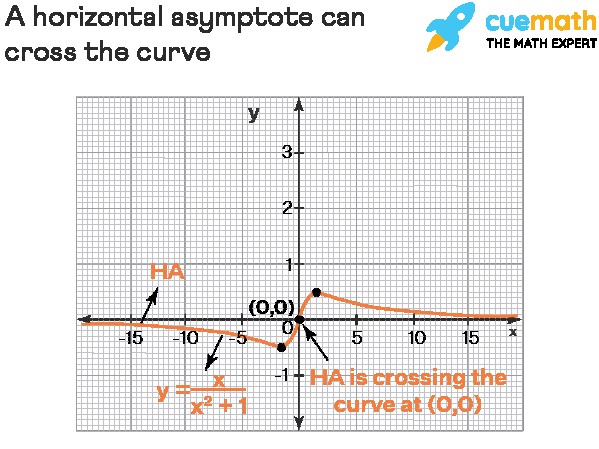
Yes, unlike vertical asymptotes, a horizontal asymptote can be crossed by the graph of the function. This means that there might be values of x for which f(x) = k, where y = k is the horizontal asymptote. Vertical asymptotes, on the other hand, are never intersected by the function’s curve.
Consider the function f(x) = x / (x2 + 1). Its horizontal asymptote is y = 0 (the x-axis). To check if the function crosses its horizontal asymptote, we set f(x) = 0:
x / (x2 + 1) = 0
This equation is satisfied when x = 0. Thus, the graph of f(x) crosses its horizontal asymptote at the point (0, 0).
Image demonstrating a graph crossing its horizontal asymptote, highlighting that intersection is possible unlike with vertical asymptotes.
Step-by-Step Guide: How to Find Horizontal Asymptotes
To find the horizontal asymptotes of a function y = f(x), follow these steps:
Step 1: Evaluate the Limit as x Approaches Infinity (x→∞)
Calculate the limit of the function as x approaches positive infinity:
lim x→∞ f(x)
Step 2: Evaluate the Limit as x Approaches Negative Infinity (x→-∞)
Calculate the limit of the function as x approaches negative infinity:
lim x→-∞ f(x)
Step 3: Determine the Horizontal Asymptotes
- If the limit in Step 1 or Step 2 (or both) results in a real number, say k, then y = k is a horizontal asymptote.
- If either limit is ±∞, it does not indicate a horizontal asymptote in that direction.
Sometimes, both limits will yield the same value, resulting in a single horizontal asymptote. To effectively evaluate these limits, understanding limit evaluation techniques is essential.
Finding Horizontal Asymptotes Graphically
Graphically, a horizontal asymptote is a horizontal line that a portion of the curve runs parallel and very close to. Remember, while the graph approaches the asymptote, it doesn’t necessarily touch it and can cross it.
Example: Find the horizontal asymptote of the function f(x) = (2x) / (x – 3).
Solution:
First, we evaluate the limit as x approaches infinity:
lim x→∞ f(x) = lim x→∞ (2x) / (x – 3)
To evaluate this limit, divide both the numerator and the denominator by the highest power of x in the denominator, which is x:
= lim x→∞ (2x/x) / ((x – 3)/x)
= lim x→∞ 2 / (1 – 3/x)
As x approaches infinity, 3/x approaches 0. Therefore:
= 2 / (1 – 0) = 2
So, y = 2 is a horizontal asymptote.
Next, evaluate the limit as x approaches negative infinity:
lim x→-∞ f(x) = lim x→-∞ (2x) / (x – 3)
Following the same process:
= lim x→-∞ 2 / (1 – 3/x) = 2 / (1 – 0) = 2
Again, we get y = 2.
Thus, the function f(x) = (2x) / (x – 3) has only one horizontal asymptote, which is y = 2.
Image showing the graph of a rational function with its horizontal asymptote, illustrating how the function approaches the asymptote as x goes to infinity.
Interestingly, horizontal asymptotes can be used to determine the range of rational functions. Since the horizontal asymptote is not a value the function reaches at extreme ends, it can help define the boundaries of the range. For the example above, the range is {y ∈ R | y ≠ 2}.
While limits provide a general method, there are quicker approaches to find horizontal asymptotes for specific types of functions.
Horizontal Asymptotes of Rational Functions: A Simpler Method
Rational functions, defined as the ratio of two polynomials, have horizontal asymptotes that can be determined by comparing the degrees of the polynomials in the numerator and the denominator. A rational function can have at most one horizontal asymptote. Here are the rules:
- Case 1: Degree of Numerator < Degree of Denominator: The horizontal asymptote is y = 0 (the x-axis).
- Case 2: Degree of Numerator = Degree of Denominator: The horizontal asymptote is y = L, where L is the ratio of the leading coefficients of the numerator and denominator.
- Case 3: Degree of Numerator > Degree of Denominator: There is no horizontal asymptote. Instead, there might be an oblique asymptote (which is not horizontal).
Let’s revisit the previous example f(x) = (2x) / (x – 3). The degree of the numerator is 1, and the degree of the denominator is also 1 (Case 2). The leading coefficient of the numerator is 2, and the leading coefficient of the denominator is 1. Thus, the horizontal asymptote is y = 2/1 = 2, which aligns with our limit calculation.
Here are more examples using these rules:
- y = (x2 + 3) / (2x): Degree of numerator (2) > degree of denominator (1). No horizontal asymptote.
- y = (2x) / (x2 + 3): Degree of numerator (1) < degree of denominator (2). Horizontal asymptote is y = 0.
- y = (2x2) / (x2 + 3): Degree of numerator (2) = degree of denominator (2). Horizontal asymptote is y = 2/1 = 2.
Horizontal Asymptotes of Exponential Functions
Exponential functions, especially in the form f(x) = abkx + c, always have exactly one horizontal asymptote. The constant c in this form represents a vertical shift of the base exponential function, and it directly corresponds to the horizontal asymptote.
- For the basic exponential function f(x) = bx, the horizontal asymptote is y = 0.
- For a transformed exponential function f(x) = abkx + c, the horizontal asymptote is y = c.
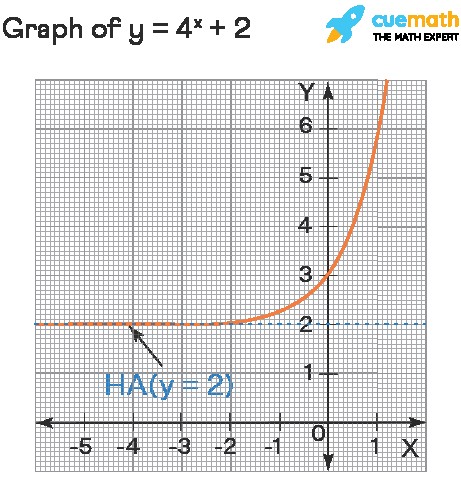
For instance, consider f(x) = 4x + 2. According to the rule, the horizontal asymptote is y = 2. This is because as x approaches negative infinity, 4x approaches 0, and f(x) approaches 0 + 2 = 2.
Image showing the graph of an exponential function with its horizontal asymptote, demonstrating how the function approaches the asymptote as x goes to negative infinity.
More examples:
- f(x) = 2x – 3: Horizontal asymptote is y = -3.
- f(x) = 3-x + 5: Horizontal asymptote is y = 5.
- f(x) = 0.52x – (2/3): Horizontal asymptote is y = -2/3.
Summary of Horizontal Asymptote Rules
Here’s a recap of the rules for finding horizontal asymptotes discussed:
- Rational Functions:
- Compare the degree of the numerator (n) and the degree of the denominator (d).
- If n < d, horizontal asymptote is y = 0.
- If n = d, horizontal asymptote is y = ratio of leading coefficients.
- If n > d, there is no horizontal asymptote.
- Compare the degree of the numerator (n) and the degree of the denominator (d).
- Exponential Functions (form f(x) = abkx + c):
- Horizontal asymptote is y = c.
- Polynomial Functions: (e.g., linear, quadratic, cubic functions)
- Polynomial functions do not have horizontal asymptotes because their limits as x approaches ±∞ are always ±∞.
- Trigonometric Functions: (e.g., sin(x), cos(x), tan(x))
- Basic trigonometric functions do not have horizontal asymptotes as they oscillate indefinitely.
- Logarithmic Functions: (e.g., ln(x), log(x))
- Basic logarithmic functions do not have horizontal asymptotes.
Important Notes on Horizontal Asymptotes:
- Not every function has a horizontal asymptote.
- A function can have a maximum of two horizontal asymptotes, which typically occurs with functions involving square roots.
- Polynomial, basic trigonometric, and basic logarithmic functions do not possess horizontal asymptotes.
Frequently Asked Questions about Horizontal Asymptotes (FAQs)
What is a Horizontal Asymptote of a Function?
The horizontal asymptote (HA) of a function y = f(x) is a horizontal line y = k that the function approaches as x approaches positive infinity (x→∞) or negative infinity (x→-∞). A function can have up to two horizontal asymptotes.
What are Horizontal Asymptote Rules?
The general method to find horizontal asymptotes is by evaluating the limits: y = lim x→∞ f(x) and y = lim x→-∞ f(x). Specific rules for certain function types include:
- Rational Functions: Compare degrees of numerator and denominator.
- Exponential Functions of the form f(x) = abkx + c: The horizontal asymptote is y = c.
What is the Difference Between Vertical and Horizontal Asymptotes?
Both vertical and horizontal asymptotes are lines that a function’s graph approaches, but they differ in orientation and behavior:
- Horizontal Asymptote: A horizontal line (y = k) describing the function’s end behavior as x approaches ±∞. A graph can cross a horizontal asymptote.
- Vertical Asymptote: A vertical line (x = k) where the function approaches infinity or negative infinity. A graph never crosses a vertical asymptote.
How to Calculate Horizontal Asymptotes?
To calculate horizontal asymptotes, evaluate the limits of the function f(x) as x approaches infinity and negative infinity: y = lim x→∞ f(x) and y = lim x→-∞ f(x). If these limits are real numbers, they define the horizontal asymptotes.
How to Find Horizontal Asymptotes of Rational Functions?
For a rational function, compare the degrees of the numerator (n) and denominator (d):
- If n < d: HA is y = 0.
- If n = d: HA is y = ratio of leading coefficients.
- If n > d: No horizontal asymptote.
How to Find Horizontal Asymptotes of Exponential Functions?
For an exponential function in the form y = abkx + c, the horizontal asymptote is simply y = c.
How to Find the Range of a Function Using Horizontal Asymptotes?
Horizontal asymptotes can help determine the range of rational functions. The horizontal asymptote value is often excluded from the range because the function approaches but does not reach this value at extreme ends. For example, if a rational function has a horizontal asymptote at y = 0, the range will exclude 0, among possibly other values due to vertical asymptotes or local extrema.
This guide provides a comprehensive explanation on how to calculate horizontal asymptotes, covering various types of functions and rules. Understanding these concepts is essential for advanced mathematical studies and applications.
Image of a teacher assisting a student, symbolizing accessible learning and simplified math concepts.