Circles are fundamental shapes in geometry, and understanding how to calculate their area is a basic mathematical skill with wide-ranging applications. Unlike squares or rectangles, circles are defined by their radius or diameter, not length and width. This guide will walk you through the methods to accurately find the area of a circle, whether you’re given the radius, diameter, or even the circumference.
Understanding the Basics of Circle Area
The area of a circle represents the space enclosed within its boundary, measured in square units. While a circle lacks straight sides, its area can be precisely calculated using specific formulas. The key to unlocking these formulas lies in understanding the relationship between a circle’s dimensions and the mathematical constant, pi (π).
The Role of Pi (π)
Pi (π) is a fundamental mathematical constant, approximately equal to 3.14159265. It represents the ratio of a circle’s circumference to its diameter and is crucial for calculating both the circumference and the area of a circle.
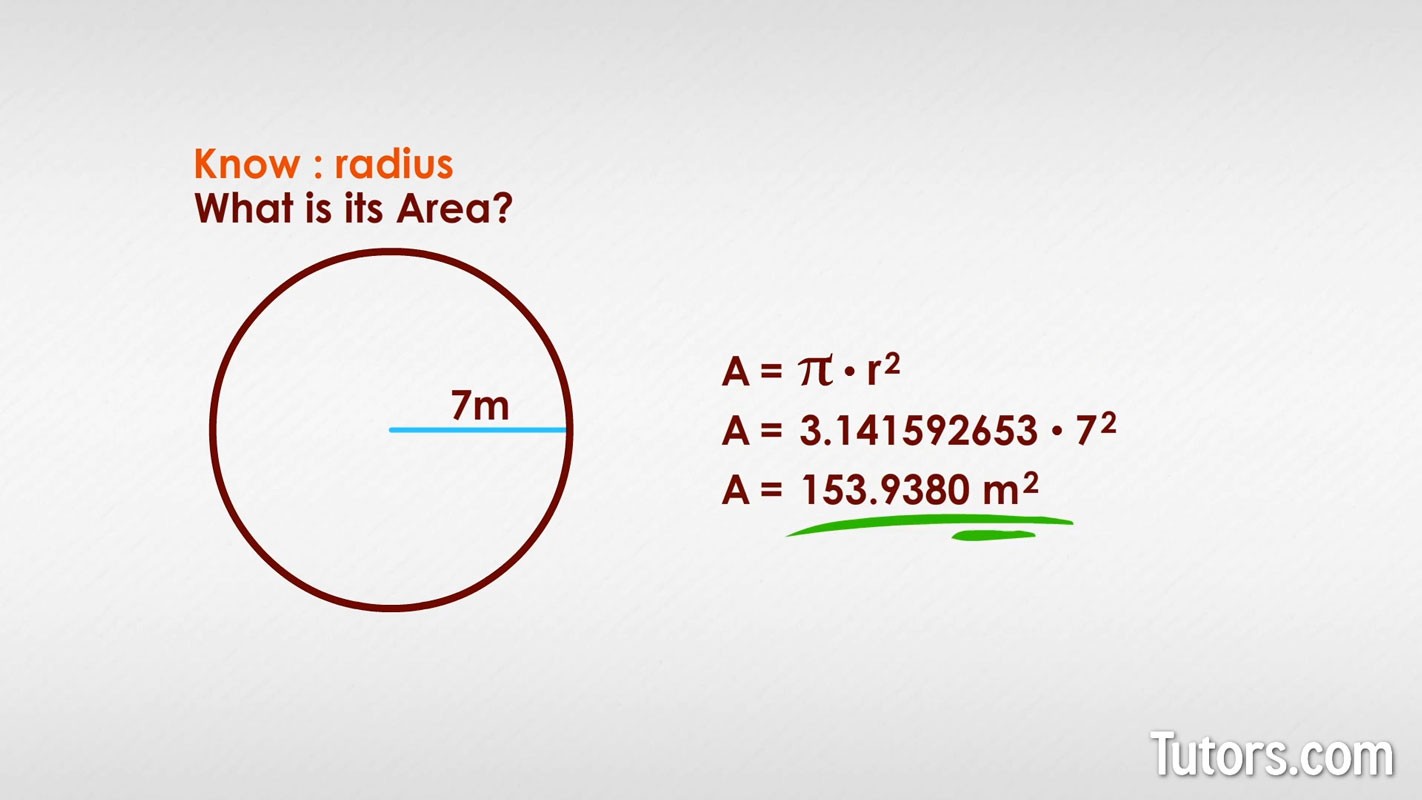
Calculating Area Using the Radius
The radius (r) of a circle is the distance from the center of the circle to any point on its circumference. If you know the radius, calculating the area is straightforward using the formula:
Area (A) = πr²
This formula states that the area of a circle is equal to pi multiplied by the square of the radius. The result will be in square units corresponding to the units of the radius (e.g., square meters if the radius is in meters, square inches if the radius is in inches).
Example:
Let’s calculate the area of a circle with a radius of 5 meters.
A = πr²
A = π × (5m)²
A = π × 25m²
A ≈ 78.54 m²
Therefore, the area of a circle with a 5-meter radius is approximately 78.54 square meters.
Calculating Area Using the Diameter
The diameter (d) of a circle is the distance across the circle passing through its center. The diameter is twice the length of the radius (d = 2r). If you are given the diameter, you can easily find the radius by dividing the diameter by 2 (r = d/2) and then use the area formula mentioned above.
Alternatively, you can use a modified formula that directly incorporates the diameter:
Area (A) = π(d/2)² or A = (π/4)d²
Example:
Consider a circular table with a diameter of 1.2 meters. Let’s find its area.
First, find the radius:
r = d/2 = 1.2m / 2 = 0.6m
Now, use the area formula:
A = πr²
A = π × (0.6m)²
A = π × 0.36m²
A ≈ 1.13 m²
Alternatively, using the diameter formula directly:
A = (π/4)d²
A = (π/4) × (1.2m)²
A = (π/4) × 1.44m²
A ≈ 1.13 m²
Both methods yield the same result: the area of the circular table is approximately 1.13 square meters.
Calculating Area Using the Circumference
The circumference (C) of a circle is the distance around its outer edge. Sometimes, you might know the circumference of a circle but not its radius or diameter. In such cases, you can still calculate the area.
First, recall the formula for circumference:
Circumference (C) = 2πr
From this, we can solve for the radius (r):
r = C / (2π)
Now, substitute this expression for ‘r’ into the area formula (A = πr²):
A = π (C / (2π))²
A = π (C² / (4π²))
A = C² / (4π)
This formula allows you to calculate the area of a circle directly from its circumference.
Example:
Imagine you have a circular garden bed, and you know its circumference is 15.7 feet. Let’s calculate the area of the garden bed.
Using the formula:
A = C² / (4π)
A = (15.7 ft)² / (4π)
A = 246.49 ft² / (4π)
A ≈ 19.61 ft²
Therefore, the area of the circular garden bed is approximately 19.61 square feet.
Practice Problems
Test your understanding with these practice problems. Remember to identify whether you are given the radius, diameter, or circumference and use the appropriate formula.
- A circular plate has a diameter of 30 centimeters. Calculate its area.
- A round swimming pool has a radius of 8 meters. What is the surface area of the pool?
- The circumference of a circular clock face is 62.8 inches. Find the area of the clock face.
- A bicycle wheel has a diameter of 700 mm. Calculate the area enclosed by the wheel.
Solutions to Practice Problems
-
Circular plate (diameter = 30 cm):
- Radius (r) = diameter / 2 = 30 cm / 2 = 15 cm
- Area (A) = πr² = π × (15 cm)² ≈ 706.86 cm²
-
Swimming pool (radius = 8 m):
- Area (A) = πr² = π × (8 m)² ≈ 201.06 m²
-
Clock face (circumference = 62.8 inches):
- Area (A) = C² / (4π) = (62.8 inches)² / (4π) ≈ 314.16 inches²
-
Bicycle wheel (diameter = 700 mm):
- Radius (r) = diameter / 2 = 700 mm / 2 = 350 mm
- Area (A) = πr² = π × (350 mm)² ≈ 384,845 mm²
Conclusion
Calculating the area of a circle is a fundamental skill in geometry. By understanding the relationship between radius, diameter, circumference, and the constant pi (π), you can confidently calculate the area of any circle using the appropriate formula. Whether you are working on math problems, home improvement projects, or real-world applications, mastering these calculations will prove to be invaluable.