Dividing decimals might seem challenging, but with the right techniques, it becomes straightforward. At HOW.EDU.VN, we understand the need for clear, expert guidance. This guide provides an in-depth explanation of decimal division, including practical examples and step-by-step instructions. Learn how to perform decimal arithmetic accurately and efficiently, transforming complex problems into manageable tasks.
Are you looking for expert advice on financial calculations or scientific applications involving decimal numbers? HOW.EDU.VN offers access to over 100 distinguished PhDs ready to provide tailored solutions. Contact us today and experience the difference expert guidance can make. With the help of experts, learn the concepts of fractional division and decimal places.
1. Understanding the Basics of Decimal Division
Decimal division involves dividing numbers that contain a decimal point. This process is essential in various fields, from finance to engineering, where precise calculations are crucial.
1.1. What Are Decimals?
A decimal is a way of representing numbers that are not whole numbers. It includes a whole number part and a fractional part, separated by a decimal point. For instance, in the number 4.5, 4 is the whole number part and .5 is the fractional part, representing five-tenths.
1.2. Why Is Decimal Division Important?
Decimal division is crucial for:
- Financial calculations: Splitting bills, calculating interest rates, and determining costs per unit.
- Scientific measurements: Ensuring accuracy in experiments and data analysis.
- Engineering applications: Designing structures and systems with precise dimensions.
- Everyday tasks: Converting units, adjusting recipes, and managing budgets.
1.3. Common Challenges in Dividing Decimals
Many people find decimal division challenging due to:
- Placement of the decimal point: Ensuring the decimal point is correctly placed in the quotient.
- Dealing with remainders: Knowing when and how to add zeroes to continue the division.
- Dividing by decimals: Converting the problem to eliminate the decimal in the divisor.
- Understanding the concept: Grasping the underlying principles of fractional parts.
2. Step-by-Step Guide to Dividing Decimals
This section breaks down the process of dividing decimals into manageable steps, ensuring clarity and accuracy.
2.1. Dividing a Decimal by a Whole Number
Dividing a decimal by a whole number is similar to regular long division, with one key difference: placing the decimal point.
Steps:
- Set up the long division: Write the decimal number (dividend) inside the division bracket and the whole number (divisor) outside.
- Divide as usual: Perform the division as you would with whole numbers, ignoring the decimal point initially.
- Place the decimal point: Once you reach the decimal point in the dividend, bring it up to the same position in the quotient (the answer).
- Continue dividing: Keep dividing until there is no remainder or until you reach the desired level of accuracy.
Example:
Divide 8.342 by 2:
4.171
2|8.342
-8
---
03
-2
---
14
-14
---
02
-2
---
0So, (8.342 ÷ 2 = 4.171).
Image illustrating the long division process of 8.342 divided by 2.
2.2. Dividing a Decimal by a Decimal
Dividing a decimal by another decimal requires an additional step to simplify the problem.
Steps:
- Eliminate the decimal in the divisor: Multiply both the divisor and the dividend by a power of 10 (10, 100, 1000, etc.) to make the divisor a whole number. Count the number of decimal places in the divisor and use that number as the exponent for 10.
- Set up the long division: Write the new dividend inside the division bracket and the new divisor outside.
- Divide as usual: Perform the division as you would with whole numbers, placing the decimal point in the quotient directly above the decimal point in the dividend.
- Continue dividing: Keep dividing until there is no remainder or until you reach the desired level of accuracy.
Example:
Divide 15.75 by 3.5:
- Eliminate the decimal: Multiply both numbers by 10 (since 3.5 has one decimal place).
- (15.75 times 10 = 157.5)
- (3.5 times 10 = 35)
- Set up the long division:
4.5
35|157.5
-140
-----
17 5
-17 5
-----
0So, (15.75 ÷ 3.5 = 4.5).
An image demonstrating how to set up decimal division with a visual example.
2.3. Dealing with Remainders
Sometimes, when dividing decimals, you will encounter a remainder. Here’s how to handle it:
Steps:
- Add a zero: Add a zero to the end of the dividend after the decimal point. This does not change the value of the number but allows you to continue dividing.
- Continue dividing: Bring down the zero and continue the division process.
- Repeat if necessary: If there is still a remainder, add another zero and continue. Repeat until the remainder is zero or you reach the desired level of accuracy.
Example:
Divide 9.67 by 5:
1.934
5|9.670
-5
---
4 6
-4 5
---
17
-15
---
20
-20
---
0So, (9.67 ÷ 5 = 1.934).
A step-by-step visual guide to managing remainders when dividing decimals.
3. Practical Examples and Applications
Decimal division is not just a theoretical concept; it has numerous real-world applications.
3.1. Calculating Gas Mileage
Let’s say you drove 350.5 miles and used 10.5 gallons of gas. To find your gas mileage (miles per gallon), you would divide the total miles by the gallons used:
(350.5 ÷ 10.5)
- Eliminate the decimal: Multiply both numbers by 10:
- (350.5 times 10 = 3505)
- (10.5 times 10 = 105)
- Divide: (3505 ÷ 105 = 33.38) (approximately)
So, your gas mileage is approximately 33.38 miles per gallon.
3.2. Splitting a Restaurant Bill
If a restaurant bill is $75.50 and you want to split it evenly among 5 people, you would divide the total bill by the number of people:
(75.50 ÷ 5)
15.10
5|75.50
-5
---
25
-25
---
05
-5
---
00
-0
---
0So, each person owes $15.10.
3.3. Converting Units
Suppose you need to convert 15.5 inches to centimeters, knowing that 1 inch is approximately 2.54 centimeters. You would multiply:
(15.5 times 2.54 = 39.37)
So, 15.5 inches is approximately 39.37 centimeters. While this is multiplication, understanding decimals is crucial for accurate conversions.
3.4. Scaling Recipes
A recipe calls for 2.5 cups of flour, but you only want to make half the recipe. You would divide:
(2.5 ÷ 2 = 1.25)
You need 1.25 cups of flour for half the recipe.
4. Tips and Tricks for Mastering Decimal Division
To become proficient in decimal division, consider these helpful tips and tricks.
4.1. Estimation
Before performing the division, estimate the answer to get a sense of what to expect. This helps you catch any significant errors in your calculations.
Example:
For (157.5 ÷ 35), round to (160 ÷ 40 = 4). Your answer should be close to 4.
4.2. Practice Regularly
The more you practice, the more comfortable you will become with the process. Start with simple problems and gradually increase the complexity.
4.3. Use Visual Aids
Visual aids like diagrams and models can help you understand the concept of decimal division, especially when teaching it to others.
Example:
Using shaded grids to represent decimals and circling groups to show division.
4.4. Check Your Work
Always double-check your work, especially when dealing with critical calculations. Use a calculator to verify your answers if possible.
4.5. Break Down Complex Problems
For complex problems, break them down into smaller, more manageable steps. This reduces the chance of making mistakes and makes the process less overwhelming.
4.6. Memorize Common Decimal Equivalents
Memorizing common decimal equivalents of fractions (e.g., 0.5 = 1/2, 0.25 = 1/4) can speed up calculations and improve your understanding.
4.7. Understand the Relationship Between Decimals and Fractions
Decimals and fractions are two ways of representing the same thing. Understanding this relationship can provide a deeper understanding of decimal division.
5. Common Mistakes to Avoid
Even with a solid understanding of the process, it’s easy to make mistakes. Here are some common errors to watch out for:
5.1. Misplacing the Decimal Point
This is one of the most common mistakes. Ensure you bring the decimal point directly up from the dividend to the quotient.
5.2. Forgetting to Multiply Both Numbers
When dividing a decimal by a decimal, remember to multiply both the divisor and the dividend by the same power of 10.
5.3. Incorrectly Adding Zeroes
Adding zeroes to the dividend should be done carefully, especially when dealing with remainders. Ensure you add them after the decimal point.
5.4. Not Checking for Reasonableness
Always check if your answer makes sense in the context of the problem. If it seems unreasonable, review your calculations.
5.5. Skipping Steps
Avoid skipping steps, especially when learning. Each step is important for ensuring accuracy.
6. Advanced Techniques in Decimal Division
For more complex scenarios, advanced techniques can be employed to enhance precision and efficiency.
6.1. Scientific Notation
When dealing with very large or very small numbers, use scientific notation to simplify the division process.
Example:
Divide (6.022 times 10^{23}) by (2.0 times 10^{3}).
- Divide the coefficients: (6.022 ÷ 2.0 = 3.011)
- Subtract the exponents: (23 – 3 = 20)
- Result: (3.011 times 10^{20})
6.2. Approximations
In some cases, an approximate answer is sufficient. Round the numbers to the nearest whole number or convenient decimal place to simplify the division.
Example:
For (12.34 ÷ 2.87), approximate to (12 ÷ 3 = 4).
6.3. Using Calculators and Software
While it’s important to understand the manual process, calculators and software can be valuable tools for complex decimal division, especially in professional settings.
7. How HOW.EDU.VN Can Help
At HOW.EDU.VN, we understand the complexities and challenges that come with decimal division and other advanced mathematical concepts. Our team of over 100 distinguished PhDs is dedicated to providing you with expert guidance and personalized solutions.
7.1. Access to Expert Advice
Connect with our PhDs who specialize in mathematics, finance, engineering, and more. Get tailored advice for your specific needs, whether it’s solving complex calculations or understanding theoretical concepts.
7.2. Personalized Solutions
Receive customized solutions designed to address your unique challenges. Our experts will work with you to break down complex problems and provide clear, actionable steps.
7.3. Save Time and Resources
Avoid the frustration of trial and error. Our experts provide efficient, accurate solutions, saving you valuable time and resources.
7.4. Ensure Confidentiality
Your privacy is our priority. We ensure that all consultations and information shared with our experts are kept confidential.
7.5. Practical, Applicable Advice
Our experts provide practical advice that you can apply immediately. Whether you’re a student, professional, or entrepreneur, you’ll receive the tools and knowledge you need to succeed.
8. Testimonials and Success Stories
Here are a few examples of how our experts at HOW.EDU.VN have helped individuals and businesses overcome complex challenges:
8.1. Financial Analysis
Challenge: A financial analyst needed to accurately calculate complex interest rates involving multiple decimals for a high-stakes investment.
Solution: One of our PhDs in finance provided a detailed breakdown of the calculations, ensuring precision and clarity.
Outcome: The analyst secured the investment with confidence, thanks to the accurate and reliable calculations.
8.2. Engineering Design
Challenge: An engineer required precise decimal calculations for designing a bridge structure, ensuring safety and stability.
Solution: Our expert in civil engineering provided step-by-step guidance, verifying each calculation to meet industry standards.
Outcome: The bridge was successfully constructed, meeting all safety requirements and performance expectations.
8.3. Academic Research
Challenge: A student struggled with decimal division while analyzing data for their thesis.
Solution: One of our academic advisors offered personalized tutoring, breaking down the concepts and providing practice problems.
Outcome: The student completed their thesis with confidence, earning high marks for their accurate data analysis.
9. Frequently Asked Questions (FAQs)
9.1. How Do You Divide Decimals?
Divide decimals by multiplying both numbers by a factor of 10 so the divisor no longer has a decimal value. Then, use long division to divide as normal. Place the decimal point in the quotient directly above the decimal point in the dividend.
Image showcasing the process of decimal division with key steps highlighted.
9.2. How Do You Divide Decimals by Whole Numbers?
Divide decimals by whole numbers the same way you divide whole numbers by each other, but put the decimal point in the answer at the same place it is at in the original number.
9.3. How Do You Divide Decimals Without a Calculator?
Divide decimals using long division, being sure to multiply by a product of 10 if there is a decimal in the divisor. Place the decimal point in the quotient directly above where it is in the dividend.
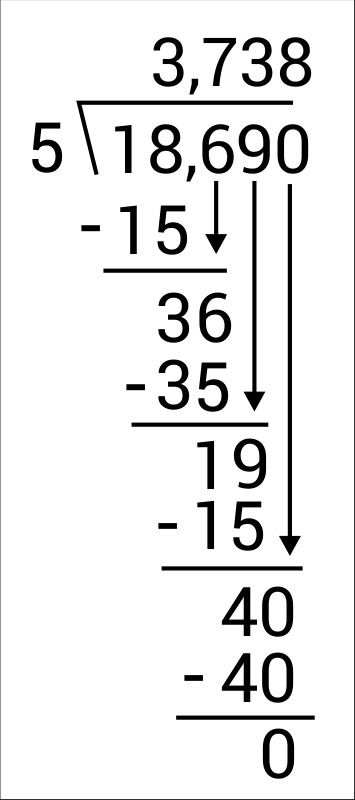Dividing decimals without a calculator
A visual representation of dividing decimals using the long division method.
9.4. How Do You Divide Decimals Using Models?
To divide decimals using models, first shade in the first number, your dividend. Then, circle groups of the second number, your divisor. The number of circled groups is your answer, or quotient.
9.5. What Do You Do With a Remainder When Dividing Decimals?
If there is a remainder when dividing decimals, add zeroes to the end of the dividend and keep dividing until there is no remainder.
9.6. Can I Get Help With Complex Decimal Division Problems?
Yes HOW.EDU.VN offers expert assistance from over 100 PhDs who can provide step-by-step guidance and personalized solutions for complex decimal division problems.
9.7. Is It Necessary to Always Eliminate the Decimal in the Divisor?
Yes, eliminating the decimal in the divisor simplifies the division process and ensures accurate results.
9.8. How Accurate Are the Approximations in Decimal Division?
The accuracy of approximations depends on the level of rounding. For more precise results, avoid excessive rounding and use more decimal places.
9.9. What Are Some Common Real-World Applications of Decimal Division?
Common applications include financial calculations, scientific measurements, engineering design, and everyday tasks like splitting bills and converting units.
10. Take the Next Step with HOW.EDU.VN
Decimal division doesn’t have to be daunting. With the right techniques and expert guidance, you can master this essential skill. At HOW.EDU.VN, we are committed to providing you with the resources and support you need to succeed.
10.1. Connect with Our Experts
Ready to take your skills to the next level? Contact us today and connect with our team of over 100 distinguished PhDs. Whether you need help with complex calculations or theoretical concepts, we’re here to provide personalized solutions.
10.2. Get Personalized Advice
Receive customized advice tailored to your unique challenges. Our experts will work with you to break down complex problems and provide clear, actionable steps.
10.3. Save Time and Resources
Avoid the frustration of trial and error. Our experts provide efficient, accurate solutions, saving you valuable time and resources.
10.4. Contact Information
Address: 456 Expertise Plaza, Consult City, CA 90210, United States
WhatsApp: +1 (310) 555-1212
Website: HOW.EDU.VN
Don’t let decimal division hold you back. Contact HOW.EDU.VN today and experience the difference expert guidance can make.
Seeking assistance with complex calculations? Unlock unparalleled expertise by consulting our distinguished team of PhDs at how.edu.vn. Contact us now for tailored solutions that drive success. Get expert insights into dividing decimals and decimal arithmetic.
