Are you grappling with understanding How To Divide Fractions? Dividing fractions may seem daunting, but it’s a manageable process when approached with the right techniques and a solid understanding of the underlying principles. HOW.EDU.VN offers expert guidance to make this mathematical operation clear and straightforward. Master the art of fraction division and enhance your math skills by learning about fraction simplification, multiplication and division relationship, and real-world applications.
1. Understanding How to Divide Fractions
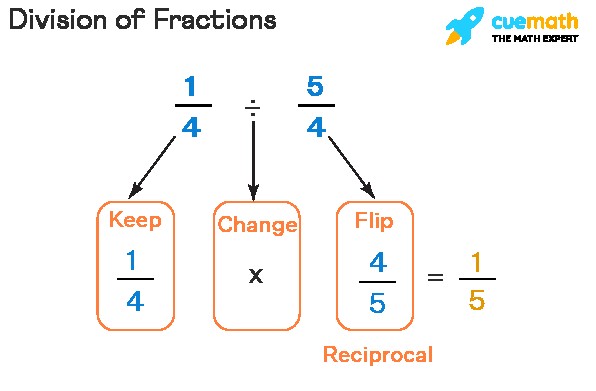
Division, in its essence, is about distributing or sharing equally. In the context of fractions, division involves determining how many times one fraction fits into another. The standard method to divide fractions is by multiplying the first fraction by the reciprocal of the second fraction. This approach simplifies the division process and makes it easier to arrive at the correct answer.
1.1 The Reciprocal Rule
The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, the reciprocal of 3/4 is 4/3. This simple inversion is key to transforming a division problem into a multiplication problem.
1.2 Step-by-Step Guide to Dividing Fractions
- Identify the Fractions: Determine which fractions you need to divide.
- Find the Reciprocal: Invert the second fraction (the divisor) to find its reciprocal.
- Multiply: Multiply the first fraction (the dividend) by the reciprocal of the second fraction.
- Simplify: Reduce the resulting fraction to its simplest form.
1.3 Example of Dividing Fractions
Consider dividing 1/2 by 3/4.
- The fractions are 1/2 and 3/4.
- The reciprocal of 3/4 is 4/3.
- Multiply 1/2 by 4/3: (1/2) * (4/3) = 4/6.
- Simplify 4/6 to 2/3.
Therefore, 1/2 divided by 3/4 equals 2/3.
2. Dividing Fractions by Fractions
When dividing a fraction by another fraction, the process remains consistent. You still need to find the reciprocal of the second fraction and multiply it by the first.
2.1 Formula for Dividing Fractions
If you are dividing x/y by a/b, the formula is:
x/y ÷ a/b = x/y b/a = (xb) / (y*a)
2.2 Practical Example
Divide 2/5 by 3/7:
- The fractions are 2/5 and 3/7.
- The reciprocal of 3/7 is 7/3.
- Multiply 2/5 by 7/3: (2/5) * (7/3) = 14/15.
- The fraction 14/15 is already in its simplest form.
Thus, 2/5 divided by 3/7 equals 14/15.
3. Division of Fractions with Whole Numbers
Dividing a fraction by a whole number involves treating the whole number as a fraction with a denominator of 1. Then, you proceed with the reciprocal and multiplication method as usual.
3.1 Converting Whole Numbers to Fractions
Any whole number ‘a’ can be written as a fraction a/1. This makes it easy to apply the division rule.
3.2 Division Process
To divide a fraction x/y by a whole number a, you would:
- Rewrite ‘a’ as a/1.
- Find the reciprocal of a/1, which is 1/a.
- Multiply x/y by 1/a: (x/y) (1/a) = x/(ya).
3.3 Example
Divide 3/4 by 6:
- Rewrite 6 as 6/1.
- The reciprocal of 6/1 is 1/6.
- Multiply 3/4 by 1/6: (3/4) * (1/6) = 3/24.
- Simplify 3/24 to 1/8.
Therefore, 3/4 divided by 6 equals 1/8.
4. Dividing Fractions with Decimals
Decimals can be converted into fractions, making it simpler to perform division. Understanding how to convert decimals to fractions is crucial for this process.
4.1 Converting Decimals to Fractions
A decimal can be expressed as a fraction by placing the decimal number over a power of 10. For example, 0.5 is 5/10, and 0.25 is 25/100.
4.2 Steps to Divide Fractions with Decimals
- Convert the decimal to a fraction.
- Apply the reciprocal rule to the second fraction.
- Multiply the first fraction by the reciprocal of the converted decimal fraction.
- Simplify the resulting fraction.
4.3 Example
Divide 1/2 by 0.75:
- Convert 0.75 to 75/100, which simplifies to 3/4.
- The reciprocal of 3/4 is 4/3.
- Multiply 1/2 by 4/3: (1/2) * (4/3) = 4/6.
- Simplify 4/6 to 2/3.
Therefore, 1/2 divided by 0.75 equals 2/3.
5. Division of Fractions and Mixed Numbers
Mixed numbers, which combine a whole number and a fraction, need to be converted into improper fractions before division can occur.
5.1 Converting Mixed Numbers to Improper Fractions
To convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator of the fraction.
- Add the result to the numerator.
- Place the sum over the original denominator.
For example, (2dfrac{1}{3}) becomes (2*3 + 1)/3 = 7/3.
5.2 Division Process
- Convert the mixed number to an improper fraction.
- Apply the reciprocal rule.
- Multiply the fractions.
- Simplify the resulting fraction.
5.3 Example
Divide 3/5 by (1dfrac{1}{2}):
- Convert (1dfrac{1}{2}) to an improper fraction: (1*2 + 1)/2 = 3/2.
- The reciprocal of 3/2 is 2/3.
- Multiply 3/5 by 2/3: (3/5) * (2/3) = 6/15.
- Simplify 6/15 to 2/5.
Therefore, 3/5 divided by (1dfrac{1}{2}) equals 2/5.
6. Advanced Strategies and Tips for Fraction Division
Mastering fraction division involves more than just knowing the basic rules. Here are some advanced strategies and tips to enhance your understanding and skills.
6.1 Simplifying Before Multiplying
Before multiplying the fractions, look for opportunities to simplify. This can involve canceling out common factors between the numerators and denominators of the fractions.
Example:
Consider ( dfrac{4}{9} div dfrac{2}{3} ).
- Rewrite as a multiplication problem: ( dfrac{4}{9} times dfrac{3}{2} ).
- Before multiplying, notice that 4 and 2 have a common factor of 2, and 9 and 3 have a common factor of 3.
- Simplify: ( dfrac{2}{3} times dfrac{1}{1} ).
- Multiply: ( dfrac{2}{3} ).
Simplifying beforehand makes the multiplication step easier and reduces the need to simplify large numbers later.
6.2 Visual Aids and Models
Visual aids can be incredibly helpful for understanding fraction division, especially for those who are new to the concept. Tools like fraction bars, pie charts, and number lines can provide a concrete representation of what it means to divide fractions.
Example:
To visualize ( dfrac{1}{2} div dfrac{1}{4} ), think of having half a pizza and wanting to know how many quarter slices you can make. Visualizing this with a pie chart makes it clear that you can make two quarter slices from half a pizza.
6.3 Real-World Applications
Connecting fraction division to real-world scenarios can make the concept more relatable and understandable.
Example:
If you have ( dfrac{3}{4} ) of a cake and want to share it equally among 3 people, each person gets ( dfrac{1}{4} ) of the cake. This is represented as ( dfrac{3}{4} div 3 = dfrac{1}{4} ).
6.4 Estimation and Checking for Reasonableness
Before performing the calculation, estimate the answer to get a sense of what a reasonable result should look like. After calculating, check if your answer is close to your estimate.
Example:
If you are dividing ( dfrac{7}{8} ) by ( dfrac{1}{2} ), you can estimate that ( dfrac{7}{8} ) is close to 1, and dividing by ( dfrac{1}{2} ) is like multiplying by 2. So, the answer should be close to 2.
6.5 Understanding the Relationship Between Multiplication and Division
Reinforce that division is the inverse operation of multiplication. Understanding this relationship can help in checking answers and solving problems more intuitively.
Example:
Since ( dfrac{2}{3} div dfrac{1}{2} = dfrac{4}{3} ), then ( dfrac{4}{3} times dfrac{1}{2} ) should equal ( dfrac{2}{3} ).
6.6 Practice with Varied Problems
The more you practice with different types of problems, the more comfortable you will become with fraction division. Work on problems that involve:
- Proper fractions
- Improper fractions
- Mixed numbers
- Decimals
- Whole numbers
6.7 Using Online Resources and Tools
There are many online resources and tools that can help you practice and understand fraction division. Websites like Khan Academy, Mathway, and others offer lessons, practice problems, and step-by-step solutions.
6.8 Common Mistakes to Avoid
- Forgetting to Take the Reciprocal: One of the most common mistakes is forgetting to invert the second fraction before multiplying.
- Simplifying Incorrectly: Ensure you are only canceling out common factors between the numerator and denominator.
- Mixing Up Numerators and Denominators: Keep track of which numbers are in the numerator and denominator, especially when dealing with mixed numbers and improper fractions.
6.9 Breaking Down Complex Problems
When faced with a complex problem involving multiple steps, break it down into smaller, more manageable parts. This makes the problem less intimidating and easier to solve.
Example:
Solve: ( dfrac{dfrac{1}{2} + dfrac{1}{3}}{dfrac{3}{4} – dfrac{1}{6}} )
- First, solve the numerator: ( dfrac{1}{2} + dfrac{1}{3} = dfrac{3}{6} + dfrac{2}{6} = dfrac{5}{6} ).
- Then, solve the denominator: ( dfrac{3}{4} – dfrac{1}{6} = dfrac{9}{12} – dfrac{2}{12} = dfrac{7}{12} ).
- Finally, divide the numerator by the denominator: ( dfrac{5}{6} div dfrac{7}{12} = dfrac{5}{6} times dfrac{12}{7} = dfrac{10}{7} ).
By breaking the problem into steps, you can tackle each part methodically and reduce the chance of making errors.
6.10 Seeking Help When Needed
Don’t hesitate to seek help from teachers, tutors, or online forums if you are struggling with fraction division. Sometimes, a different explanation or approach can make all the difference.
By employing these advanced strategies and tips, you can deepen your understanding of fraction division and tackle even the most challenging problems with confidence.
7. Real-Life Applications of Dividing Fractions
Understanding how to divide fractions is not just an academic exercise; it has numerous practical applications in everyday life. Here are some real-life scenarios where dividing fractions can be incredibly useful.
7.1 Cooking and Baking
Recipes often need to be adjusted based on the number of servings required. Dividing fractions is essential when halving or doubling recipes.
Example:
A recipe calls for ( dfrac{2}{3} ) cup of flour, but you only want to make half the recipe. You need to divide ( dfrac{2}{3} ) by 2:
- ( dfrac{2}{3} div 2 = dfrac{2}{3} times dfrac{1}{2} = dfrac{1}{3} )
- You would need ( dfrac{1}{3} ) cup of flour.
7.2 Home Improvement Projects
When working on home improvement projects, you might need to divide materials or measurements.
Example:
You have a piece of wood that is ( dfrac{3}{4} ) of a meter long, and you need to cut it into 5 equal pieces. To find the length of each piece, you divide ( dfrac{3}{4} ) by 5:
- ( dfrac{3}{4} div 5 = dfrac{3}{4} times dfrac{1}{5} = dfrac{3}{20} )
- Each piece should be ( dfrac{3}{20} ) of a meter long.
7.3 Sharing and Distribution
Dividing fractions is useful when you need to share a quantity equally among a group of people.
Example:
You have ( dfrac{5}{8} ) of a pizza left and want to share it among 4 friends. To find out how much each friend gets, you divide ( dfrac{5}{8} ) by 4:
- ( dfrac{5}{8} div 4 = dfrac{5}{8} times dfrac{1}{4} = dfrac{5}{32} )
- Each friend gets ( dfrac{5}{32} ) of the pizza.
7.4 Calculating Time and Distance
Dividing fractions can help in calculating time and distance, especially in scenarios involving fractions of hours or miles.
Example:
If you can run ( dfrac{3}{5} ) of a mile in ( dfrac{1}{4} ) of an hour, how far can you run in a full hour?
- To find the distance per hour, you divide ( dfrac{3}{5} ) by ( dfrac{1}{4} ):
- ( dfrac{3}{5} div dfrac{1}{4} = dfrac{3}{5} times dfrac{4}{1} = dfrac{12}{5} = 2dfrac{2}{5} )
- You can run ( 2dfrac{2}{5} ) miles in an hour.
7.5 Financial Planning
Dividing fractions can be used in financial planning, such as when calculating investment returns or dividing expenses.
Example:
You invest ( dfrac{1}{3} ) of your savings in stocks and want to divide that portion equally among 5 different stocks. To find out what fraction of your total savings goes into each stock, you divide ( dfrac{1}{3} ) by 5:
- ( dfrac{1}{3} div 5 = dfrac{1}{3} times dfrac{1}{5} = dfrac{1}{15} )
- Each stock gets ( dfrac{1}{15} ) of your total savings.
7.6 Construction and Carpentry
In construction and carpentry, precise measurements are crucial. Dividing fractions helps in ensuring accuracy when cutting materials.
Example:
You need to divide a ( dfrac{7}{8} )-inch bolt into 3 equal parts for a project. To find the length of each part, you divide ( dfrac{7}{8} ) by 3:
- ( dfrac{7}{8} div 3 = dfrac{7}{8} times dfrac{1}{3} = dfrac{7}{24} )
- Each part should be ( dfrac{7}{24} ) inches long.
7.7 Gardening
Dividing fractions can be useful in gardening for spacing plants or distributing fertilizer.
Example:
You have ( dfrac{2}{5} ) of a bag of fertilizer and want to spread it evenly over 4 garden beds. To find out how much fertilizer each bed gets, you divide ( dfrac{2}{5} ) by 4:
- ( dfrac{2}{5} div 4 = dfrac{2}{5} times dfrac{1}{4} = dfrac{1}{10} )
- Each garden bed gets ( dfrac{1}{10} ) of the bag of fertilizer.
7.8 Sewing and Crafts
Dividing fractions is often necessary in sewing and crafting for measuring fabric or dividing materials.
Example:
You have ( dfrac{5}{6} ) of a yard of fabric and want to make 2 identical doll dresses. To find out how much fabric each dress requires, you divide ( dfrac{5}{6} ) by 2:
- ( dfrac{5}{6} div 2 = dfrac{5}{6} times dfrac{1}{2} = dfrac{5}{12} )
- Each dress requires ( dfrac{5}{12} ) of a yard of fabric.
These examples illustrate that dividing fractions is not just a mathematical concept but a practical skill that is used in many aspects of daily life. By understanding how to divide fractions, you can solve problems more efficiently and make informed decisions in various situations.
8. Why Choose HOW.EDU.VN for Math Guidance
Navigating the complexities of mathematics, especially topics like dividing fractions, can be significantly easier with the right guidance. HOW.EDU.VN stands out as a premier platform for gaining expert advice and solutions to your mathematical challenges. Here are several compelling reasons why you should consider seeking assistance from our team of esteemed PhD experts.
8.1 Access to Top-Tier Experts
HOW.EDU.VN boasts a network of over 100 PhD-level experts across various fields. These professionals bring years of experience and in-depth knowledge, ensuring you receive the most accurate and reliable guidance.
8.2 Personalized Solutions
We understand that every learner has unique needs and challenges. Our experts provide personalized solutions tailored to your specific requirements, ensuring that you grasp the concepts effectively and efficiently.
8.3 Comprehensive Support
Whether you’re struggling with basic fraction division or more complex mathematical concepts, HOW.EDU.VN offers comprehensive support. Our experts can assist with:
- Step-by-step explanations
- Problem-solving strategies
- Conceptual understanding
- Real-world applications
8.4 Time and Cost Efficiency
Finding high-quality consultation can be time-consuming and expensive. HOW.EDU.VN streamlines this process by connecting you directly with qualified experts, saving you both time and money.
8.5 Confidential and Reliable Advice
We prioritize the confidentiality and reliability of our consultations. You can trust that your questions and concerns will be addressed with the utmost professionalism and discretion.
8.6 Diverse Expertise
Our experts come from diverse backgrounds and specializations, ensuring that we can address a wide range of mathematical topics and challenges. Whether you need help with arithmetic, algebra, calculus, or beyond, HOW.EDU.VN has the right expert for you.
8.7 Practical and Actionable Insights
Our goal is not just to provide answers but to equip you with the knowledge and skills to solve problems independently. Our experts offer practical and actionable insights that you can apply to future challenges.
8.8 Testimonials and Success Stories
Many students and professionals have benefited from the expertise available at HOW.EDU.VN. Their success stories serve as a testament to the quality and effectiveness of our services.
8.9 Cutting-Edge Information
In today’s rapidly evolving world, staying updated with the latest advancements is crucial. Our experts are committed to continuous learning and can provide you with cutting-edge information and techniques.
8.10 Convenient Access
HOW.EDU.VN offers convenient access to experts from anywhere in the world. Whether you prefer online consultations, email support, or phone calls, we provide flexible options to suit your needs.
By choosing HOW.EDU.VN, you’re not just getting answers; you’re investing in your education and professional growth. Our team of PhD experts is dedicated to helping you achieve your goals and overcome any challenges you may face.
9. Examples of Dividing Fractions
9.1 Example 1: Dividing Two Proper Fractions
Problem: Calculate ( dfrac{3}{5} div dfrac{2}{7} ).
Solution:
- Identify the Fractions: The fractions are ( dfrac{3}{5} ) and ( dfrac{2}{7} ).
- Find the Reciprocal: The reciprocal of ( dfrac{2}{7} ) is ( dfrac{7}{2} ).
- Multiply: Multiply ( dfrac{3}{5} ) by ( dfrac{7}{2} ): ( dfrac{3}{5} times dfrac{7}{2} = dfrac{3 times 7}{5 times 2} = dfrac{21}{10} ).
- Simplify: The fraction ( dfrac{21}{10} ) is an improper fraction. Convert it to a mixed number: ( 2dfrac{1}{10} ).
Answer: ( dfrac{3}{5} div dfrac{2}{7} = 2dfrac{1}{10} ).
9.2 Example 2: Dividing a Fraction by a Whole Number
Problem: Calculate ( dfrac{2}{3} div 4 ).
Solution:
- Identify the Fraction and Whole Number: The fraction is ( dfrac{2}{3} ) and the whole number is 4.
- Convert the Whole Number to a Fraction: Write 4 as ( dfrac{4}{1} ).
- Find the Reciprocal: The reciprocal of ( dfrac{4}{1} ) is ( dfrac{1}{4} ).
- Multiply: Multiply ( dfrac{2}{3} ) by ( dfrac{1}{4} ): ( dfrac{2}{3} times dfrac{1}{4} = dfrac{2 times 1}{3 times 4} = dfrac{2}{12} ).
- Simplify: Simplify ( dfrac{2}{12} ) by dividing both numerator and denominator by 2: ( dfrac{2 div 2}{12 div 2} = dfrac{1}{6} ).
Answer: ( dfrac{2}{3} div 4 = dfrac{1}{6} ).
9.3 Example 3: Dividing a Fraction by a Decimal
Problem: Calculate ( dfrac{5}{8} div 0.25 ).
Solution:
- Identify the Fraction and Decimal: The fraction is ( dfrac{5}{8} ) and the decimal is 0.25.
- Convert the Decimal to a Fraction: Write 0.25 as ( dfrac{25}{100} ), which simplifies to ( dfrac{1}{4} ).
- Find the Reciprocal: The reciprocal of ( dfrac{1}{4} ) is ( dfrac{4}{1} ).
- Multiply: Multiply ( dfrac{5}{8} ) by ( dfrac{4}{1} ): ( dfrac{5}{8} times dfrac{4}{1} = dfrac{5 times 4}{8 times 1} = dfrac{20}{8} ).
- Simplify: Simplify ( dfrac{20}{8} ) by dividing both numerator and denominator by 4: ( dfrac{20 div 4}{8 div 4} = dfrac{5}{2} ). Convert ( dfrac{5}{2} ) to a mixed number: ( 2dfrac{1}{2} ).
Answer: ( dfrac{5}{8} div 0.25 = 2dfrac{1}{2} ).
9.4 Example 4: Dividing a Fraction by a Mixed Number
Problem: Calculate ( dfrac{3}{4} div 1dfrac{1}{2} ).
Solution:
- Identify the Fraction and Mixed Number: The fraction is ( dfrac{3}{4} ) and the mixed number is ( 1dfrac{1}{2} ).
- Convert the Mixed Number to an Improper Fraction: Convert ( 1dfrac{1}{2} ) to ( dfrac{(1 times 2) + 1}{2} = dfrac{3}{2} ).
- Find the Reciprocal: The reciprocal of ( dfrac{3}{2} ) is ( dfrac{2}{3} ).
- Multiply: Multiply ( dfrac{3}{4} ) by ( dfrac{2}{3} ): ( dfrac{3}{4} times dfrac{2}{3} = dfrac{3 times 2}{4 times 3} = dfrac{6}{12} ).
- Simplify: Simplify ( dfrac{6}{12} ) by dividing both numerator and denominator by 6: ( dfrac{6 div 6}{12 div 6} = dfrac{1}{2} ).
Answer: ( dfrac{3}{4} div 1dfrac{1}{2} = dfrac{1}{2} ).
9.5 Example 5: Complex Fraction Division
Problem: Calculate ( dfrac{dfrac{2}{5}}{dfrac{3}{4}} ).
Solution:
- Identify the Fractions: The complex fraction is ( dfrac{dfrac{2}{5}}{dfrac{3}{4}} ), which means ( dfrac{2}{5} div dfrac{3}{4} ).
- Find the Reciprocal: The reciprocal of ( dfrac{3}{4} ) is ( dfrac{4}{3} ).
- Multiply: Multiply ( dfrac{2}{5} ) by ( dfrac{4}{3} ): ( dfrac{2}{5} times dfrac{4}{3} = dfrac{2 times 4}{5 times 3} = dfrac{8}{15} ).
- Simplify: The fraction ( dfrac{8}{15} ) is already in its simplest form.
Answer: ( dfrac{dfrac{2}{5}}{dfrac{3}{4}} = dfrac{8}{15} ).
These examples provide a comprehensive understanding of how to divide various types of fractions, reinforcing the basic steps and techniques.
10. Division of Fractions: Frequently Asked Questions (FAQs)
10.1 What is the Basic Principle Behind Dividing Fractions?
The fundamental principle is to multiply the first fraction (the dividend) by the reciprocal of the second fraction (the divisor).
10.2 How Do I Find the Reciprocal of a Fraction?
To find the reciprocal of a fraction, simply swap the numerator and the denominator. For example, the reciprocal of ( dfrac{a}{b} ) is ( dfrac{b}{a} ).
10.3 Can You Divide a Fraction by Zero?
No, division by zero is undefined in mathematics.
10.4 How Do I Divide a Fraction by a Whole Number?
Treat the whole number as a fraction with a denominator of 1, then multiply the first fraction by the reciprocal of this fraction.
10.5 What Steps Should I Take to Divide Mixed Numbers?
First, convert the mixed numbers to improper fractions, then multiply the first fraction by the reciprocal of the second.
10.6 How Do I Divide Fractions with Different Denominators?
When dividing fractions, the denominators do not need to be the same. You can proceed directly with finding the reciprocal and multiplying.
10.7 What is a Complex Fraction, and How Do I Divide It?
A complex fraction is a fraction where the numerator, denominator, or both contain fractions. To divide it, simplify the numerator and denominator separately, then divide the simplified numerator by the simplified denominator.
10.8 How Can I Visually Represent Dividing Fractions?
Visual aids like fraction bars or pie charts can help. For instance, to visualize ( dfrac{1}{2} div dfrac{1}{4} ), think of how many quarter slices fit into half a pie.
10.9 What Are Some Common Mistakes to Avoid When Dividing Fractions?
Common mistakes include forgetting to take the reciprocal, simplifying fractions incorrectly, and mixing up numerators and denominators.
10.10 How Can I Practice Dividing Fractions?
Use online resources, worksheets, and real-world problems to practice. The more you practice, the more comfortable you will become with the process.
Still have questions or need personalized assistance with dividing fractions? Our team of PhD experts at HOW.EDU.VN is ready to help. Contact us today for expert guidance and tailored solutions to your mathematical challenges.
Don’t let fraction division hold you back. Connect with our expert PhDs at HOW.EDU.VN and get the personalized guidance you need to master this essential skill. Reach out to us at 456 Expertise Plaza, Consult City, CA 90210, United States, or contact us via WhatsApp at +1 (310) 555-1212. Visit our website at how.edu.vn for more information. Let us help you transform your challenges into triumphs.