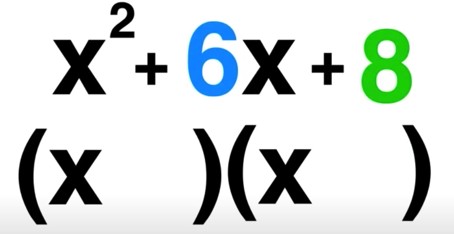Factoring trinomials is a fundamental skill in algebra, crucial for solving equations and simplifying expressions. This comprehensive guide, brought to you by HOW.EDU.VN, provides a clear, step-by-step approach to mastering this skill, whether ‘a’ equals 1 or not. Learn to simplify complex algebraic expressions with confidence by unlocking the secrets to polynomial factorization, quadratic expressions and binomial factors.
1. Understanding Trinomials: Key Definitions
Before diving into the factoring process, it’s essential to grasp the basic definition of a trinomial and the roles of its coefficients.
1.1 What is a Trinomial?
A trinomial is a polynomial expression consisting of three terms. These terms typically follow a specific structure:
- ax² term: The quadratic term, where ‘a’ is the coefficient.
- bx term: The linear term, where ‘b’ is the coefficient.
- c: The constant term.
For instance, in the trinomial 3x² + 5x + 2, the values are a=3, b=5, and c=2. Recognizing these components is the first step towards successful factorization.
1.2 The Significance of a, b, and c
Understanding the roles of ‘a’, ‘b’, and ‘c’ is crucial for identifying the structure of the trinomial and applying the correct factoring techniques.
- ‘a’: The coefficient of the x² term, which determines the complexity of the factoring process. When a=1, the factoring is simpler.
- ‘b’: The coefficient of the x term, influencing the sum aspect of the factors.
- ‘c’: The constant term, dictating the product aspect of the factors.
2. Factoring Trinomials When a = 1
When the leading coefficient, ‘a’, equals 1, factoring becomes more straightforward. This section will guide you through the process with illustrative examples.
2.1 Step-by-Step Method for Factoring When a = 1
The following three steps will help you master factoring trinomials where a = 1:
- Identify b and c: Determine the values of ‘b’ (the coefficient of the x term) and ‘c’ (the constant term) in the trinomial x² + bx + c.
- Find two numbers: Discover two numbers that add up to ‘b’ and multiply to ‘c’. This may require some trial and error.
- Write the factors: Use the identified numbers to create two binomial factors in the form (x + number 1) and (x + number 2).
2.2 Factoring Trinomials Example 1
Let’s apply these steps to factor the trinomial x² + 7x + 12.
- Identify b and c: In this trinomial, b = 7 and c = 12.
- Find two numbers: We need two numbers that add up to 7 and multiply to 12. After considering the factors of 12 (1×12, 2×6, 3×4), we find that 3 and 4 satisfy both conditions (3 + 4 = 7 and 3 x 4 = 12).
- Write the factors: The factored form is (x + 3)(x + 4).
To verify the answer, multiply the two binomials together:
(x + 3)(x + 4) = x² + 4x + 3x + 12 = x² + 7x + 12
This matches the original trinomial, confirming the correctness of the factors.
2.3 Factoring Trinomials Example 2
Consider the trinomial x² + 5x + 6.
- Identify b and c: Here, b = 5 and c = 6.
- Find two numbers: We need two numbers that add up to 5 and multiply to 6. The factors of 6 are 1×6 and 2×3. The numbers 2 and 3 meet both requirements (2 + 3 = 5 and 2 x 3 = 6).
- Write the factors: The factored form is (x + 2)(x + 3).
2.4 Factoring Trinomials Example 3
Factor the trinomial x² – 2x – 8.
- Identify b and c: In this case, b = -2 and c = -8.
- Find two numbers: We need two numbers that add up to -2 and multiply to -8. The factors of -8 are -1×8, 1x-8, -2×4, and 2x-4. The numbers 2 and -4 satisfy both conditions (2 + (-4) = -2 and 2 x -4 = -8).
- Write the factors: The factored form is (x + 2)(x – 4).
3. Factoring Trinomials When a ≠ 1
When the leading coefficient ‘a’ is not equal to 1, the factoring process becomes more complex, often requiring additional steps. This section will explore the methods to handle such trinomials, enhancing your problem-solving skills.
3.1 The “ac” Method: A Detailed Approach
The “ac” method is a common technique used to factor trinomials of the form ax² + bx + c when a ≠ 1. Here’s a step-by-step breakdown:
- Multiply a and c: Calculate the product of ‘a’ and ‘c’.
- Find two numbers: Find two numbers that multiply to the result from step 1 (ac) and add up to ‘b’.
- Rewrite the middle term: Rewrite the middle term (bx) using the two numbers found in step 2.
- Factor by grouping: Group the first two terms and the last two terms, then factor out the greatest common factor (GCF) from each group.
- Final factorization: Write the final factored form using the common binomial factor.
3.2 Factoring Trinomials Example 1: Using the “ac” Method
Let’s factor the trinomial 2x² + 7x + 3 using the “ac” method.
- Multiply a and c: a = 2, c = 3, so ac = 2 x 3 = 6.
- Find two numbers: We need two numbers that multiply to 6 and add up to 7. The numbers are 1 and 6 (1 x 6 = 6 and 1 + 6 = 7).
- Rewrite the middle term: Rewrite 7x as 1x + 6x. The trinomial becomes 2x² + 1x + 6x + 3.
- Factor by grouping:
- Group the first two terms: (2x² + 1x). Factor out the GCF, which is x: x(2x + 1).
- Group the last two terms: (6x + 3). Factor out the GCF, which is 3: 3(2x + 1).
- Final factorization: The expression is now x(2x + 1) + 3(2x + 1). Factor out the common binomial factor (2x + 1): (2x + 1)(x + 3).
Thus, the factored form of 2x² + 7x + 3 is (2x + 1)(x + 3).
3.3 Factoring Trinomials Example 2: Using the “ac” Method
Consider the trinomial 3x² – 8x + 4.
- Multiply a and c: a = 3, c = 4, so ac = 3 x 4 = 12.
- Find two numbers: We need two numbers that multiply to 12 and add up to -8. The numbers are -2 and -6 (-2 x -6 = 12 and -2 + -6 = -8).
- Rewrite the middle term: Rewrite -8x as -2x – 6x. The trinomial becomes 3x² – 2x – 6x + 4.
- Factor by grouping:
- Group the first two terms: (3x² – 2x). Factor out the GCF, which is x: x(3x – 2).
- Group the last two terms: (-6x + 4). Factor out the GCF, which is -2: -2(3x – 2).
- Final factorization: The expression is now x(3x – 2) – 2(3x – 2). Factor out the common binomial factor (3x – 2): (3x – 2)(x – 2).
Thus, the factored form of 3x² – 8x + 4 is (3x – 2)(x – 2).
3.4 Factoring Trinomials Example 3: Using the “ac” Method
Factor the trinomial 4x² + 11x – 3.
- Multiply a and c: a = 4, c = -3, so ac = 4 x -3 = -12.
- Find two numbers: We need two numbers that multiply to -12 and add up to 11. The numbers are -1 and 12 (-1 x 12 = -12 and -1 + 12 = 11).
- Rewrite the middle term: Rewrite 11x as -1x + 12x. The trinomial becomes 4x² – 1x + 12x – 3.
- Factor by grouping:
- Group the first two terms: (4x² – 1x). Factor out the GCF, which is x: x(4x – 1).
- Group the last two terms: (12x – 3). Factor out the GCF, which is 3: 3(4x – 1).
- Final factorization: The expression is now x(4x – 1) + 3(4x – 1). Factor out the common binomial factor (4x – 1): (4x – 1)(x + 3).
Thus, the factored form of 4x² + 11x – 3 is (4x – 1)(x + 3).
4. Alternative Method: Completing the Square
Completing the square is another powerful method for factoring trinomials, particularly useful when solving quadratic equations.
4.1 The Completing the Square Formula: An Overview
Completing the square involves transforming a quadratic equation into a perfect square trinomial. This is achieved by adding and subtracting a specific value to both sides of the equation.
4.2 Steps to Completing the Square
Here’s how to complete the square:
- Ensure a = 1: If a ≠ 1, divide the entire equation by ‘a’.
- Move the constant: Move the constant term ‘c’ to the right side of the equation.
- Calculate the value to complete the square: Take half of the coefficient of the x term (b/2), square it ((b/2)²), and add this value to both sides of the equation.
- Factor the perfect square trinomial: The left side of the equation should now be a perfect square trinomial, which can be factored into (x + b/2)².
- Solve for x: Take the square root of both sides and solve for x.
4.3 Completing the Square Example
Solve the quadratic equation x² + 6x + 5 = 0 by completing the square.
- Ensure a = 1: In this case, a = 1.
- Move the constant: Subtract 5 from both sides: x² + 6x = -5.
- Calculate the value to complete the square: Half of 6 is 3, and 3² = 9. Add 9 to both sides: x² + 6x + 9 = -5 + 9.
- Factor the perfect square trinomial: The left side factors into (x + 3)²: (x + 3)² = 4.
- Solve for x: Take the square root of both sides: x + 3 = ±2.
- x + 3 = 2 => x = -1
- x + 3 = -2 => x = -5
Thus, the solutions are x = -1 and x = -5.
4.4 The Power of Expert Guidance
While these methods provide a solid foundation for factoring trinomials, the complexities of algebra can sometimes be daunting. Seeking advice from experienced professionals ensures that your mathematical challenges are addressed with precision and expertise. At HOW.EDU.VN, you can connect directly with top-tier experts who offer tailored solutions and guidance.
5. Benefits of Consulting with Experts at HOW.EDU.VN
Navigating the complexities of factoring trinomials and other algebraic challenges can be significantly easier with expert guidance. HOW.EDU.VN offers unparalleled access to leading professionals who can provide customized solutions and insights. Here are some key benefits of consulting with experts through our platform:
- Personalized Solutions: Receive tailored strategies that address your specific challenges, ensuring effective learning and problem-solving.
- Expert Insights: Gain access to in-depth knowledge and practical tips from experienced mathematicians and educators.
- Time Efficiency: Save time and avoid frustration by getting clear, concise guidance that cuts through the confusion.
- Confidence Building: Enhance your understanding and confidence in tackling algebraic problems, empowering you to excel in your studies or professional endeavors.
- 24/7 Availability: Our services are available around the clock, allowing you to get the help you need whenever you need it.
5.1 Real-World Applications and Expert Testimonials
Factoring trinomials is not just an academic exercise; it has numerous real-world applications.
- Engineering: Engineers use factoring to design structures and solve complex equations.
- Finance: Financial analysts use factoring to model investment strategies and manage risk.
- Computer Science: Computer scientists apply factoring in algorithm design and optimization.
5.2 Overcoming Common Challenges with Expert Assistance
Many individuals face challenges when factoring trinomials, such as:
- Difficulty identifying factors: Struggling to find the correct numbers that add up to ‘b’ and multiply to ‘c’.
- Confusion with negative signs: Making errors when dealing with negative coefficients.
- Applying the “ac” method: Finding it hard to rewrite the middle term and factor by grouping.
With the assistance of experts at HOW.EDU.VN, these challenges can be overcome through personalized guidance and targeted practice.
6. Why Choose HOW.EDU.VN for Expert Math Assistance?
HOW.EDU.VN stands out as a premier destination for individuals seeking expert advice and solutions in mathematics. Here’s why you should choose us:
- Top-Tier Experts: We connect you with seasoned mathematicians, academics, and industry professionals who possess extensive knowledge and a proven track record of success.
- Customized Solutions: We understand that every individual has unique needs. Our experts provide tailored solutions that address your specific challenges.
- Comprehensive Support: From basic algebra to advanced calculus, we offer comprehensive support across all areas of mathematics.
- Convenient Access: Our platform allows you to connect with experts anytime, anywhere, ensuring you get the help you need when you need it.
- Guaranteed Satisfaction: We are committed to providing high-quality service and ensuring your satisfaction.
6.1 Success Stories from Satisfied Clients
“I was struggling with factoring trinomials and feeling overwhelmed. Thanks to HOW.EDU.VN, I connected with an expert who explained the concepts clearly and provided step-by-step guidance. Now, I feel confident in my ability to solve these problems.” – Sarah J.
“As an engineer, I often need to use factoring in my work. The experts at HOW.EDU.VN helped me refresh my skills and provided practical insights that have been invaluable. I highly recommend their services.” – Mark L.
7. Frequently Asked Questions (FAQs)
Q1: What is a trinomial, and why is it important to learn how to factor it?
A: A trinomial is a polynomial with three terms, usually in the form ax² + bx + c. Factoring trinomials is crucial because it simplifies complex algebraic expressions, helps solve quadratic equations, and is fundamental in many areas of mathematics and science.
Q2: How do I factor a trinomial when a = 1?
A: When a = 1, you need to find two numbers that add up to ‘b’ and multiply to ‘c’. Once you find these numbers, you can write the factored form as (x + number 1)(x + number 2).
Q3: What is the “ac” method, and when should I use it?
A: The “ac” method is used when factoring trinomials in the form ax² + bx + c, where a ≠ 1. It involves multiplying ‘a’ and ‘c’, finding two numbers that multiply to ‘ac’ and add up to ‘b’, rewriting the middle term, and then factoring by grouping.
Q4: Can you explain the completing the square method for factoring trinomials?
A: Completing the square is a method used to solve quadratic equations by transforming them into perfect square trinomials. It involves adding and subtracting a specific value to both sides of the equation to create a perfect square, which can then be easily factored.
Q5: How can HOW.EDU.VN help me with factoring trinomials?
A: HOW.EDU.VN connects you with experienced experts who can provide personalized guidance, step-by-step solutions, and practical insights to help you master factoring trinomials and other algebraic concepts.
Q6: What are the benefits of consulting with an expert for math problems?
A: Consulting with an expert offers personalized solutions, expert insights, time efficiency, confidence building, and 24/7 availability, ensuring you get the help you need when you need it.
Q7: Are the experts at HOW.EDU.VN qualified to help with advanced math topics?
A: Yes, HOW.EDU.VN works with top-tier mathematicians, academics, and industry professionals who have extensive knowledge and experience in various areas of mathematics, including advanced topics.
Q8: How can I get started with HOW.EDU.VN?
A: Simply visit our website at HOW.EDU.VN to explore our services and connect with an expert. You can also contact us via WhatsApp at +1 (310) 555-1212 or visit our office at 456 Expertise Plaza, Consult City, CA 90210, United States.
Q9: What if I have a math problem that is not related to factoring trinomials?
A: HOW.EDU.VN offers comprehensive support across all areas of mathematics. Whether you need help with algebra, calculus, geometry, or any other math topic, our experts are ready to assist you.
Q10: How do I know that the advice I receive from HOW.EDU.VN is reliable?
A: HOW.EDU.VN is committed to providing high-quality service and ensuring your satisfaction. Our experts are carefully vetted to ensure they possess the knowledge, experience, and communication skills necessary to provide accurate and effective guidance.
8. Conclusion: Mastering Factoring Trinomials with HOW.EDU.VN
Mastering factoring trinomials is an essential step in your mathematical journey. Whether you are a student, a professional, or simply someone who enjoys solving problems, the ability to factor trinomials will open up new possibilities and enhance your problem-solving skills. With the step-by-step methods and expert guidance available at HOW.EDU.VN, you can confidently tackle any trinomial that comes your way.
8.1 Final Thoughts and Recommendations
Factoring trinomials may seem daunting at first, but with practice and the right guidance, it can become second nature. Remember to:
- Practice regularly: The more you practice, the more comfortable you will become with the different methods and techniques.
- Seek help when needed: Don’t hesitate to reach out to experts at HOW.EDU.VN when you encounter challenges.
- Review the basics: Make sure you have a solid understanding of the fundamental concepts, such as the definition of a trinomial and the roles of ‘a’, ‘b’, and ‘c’.
8.2 Take Action Today
Ready to take your math skills to the next level? Visit HOW.EDU.VN today and connect with an expert who can provide personalized guidance and support. Whether you are struggling with factoring trinomials or need help with other math topics, our team is here to help you succeed.
Don’t wait! Contact us today:
- Address: 456 Expertise Plaza, Consult City, CA 90210, United States
- WhatsApp: +1 (310) 555-1212
- Website: HOW.EDU.VN
Unlock your potential and achieve your goals with the help of the experts at how.edu.vn. Your journey to math mastery starts here.