Finding the area of a circle might seem complex, but it’s a fundamental concept with practical applications. At HOW.EDU.VN, we provide expert guidance to help you master this skill. This comprehensive guide explains how to calculate the area of a circle using different known values, such as radius, diameter, or circumference. Discover the secrets to calculating circular area, circle measurement, and area calculation today.
1. Understanding the Basics of Circle Area
The area of a circle refers to the amount of space enclosed within its boundary. Unlike squares or rectangles, a circle’s area is defined by its unique property: all points on the circle are equidistant from the center. This distance is known as the radius, which is crucial in calculating the area.
1.1. Defining Circle Terminology
Before diving into the formulas, it’s essential to understand the key terms associated with circles:
- Radius (r): The distance from the center of the circle to any point on its edge.
- Diameter (d): The distance across the circle passing through the center. It is twice the length of the radius (d = 2r).
- Circumference (C): The distance around the circle.
- Pi (π): A mathematical constant approximately equal to 3.14159, representing the ratio of a circle’s circumference to its diameter.
1.2. Why is Knowing the Area of a Circle Important?
Understanding how to calculate the area of a circle has various practical applications across multiple fields:
- Engineering: Calculating the cross-sectional area of pipes or cylindrical structures.
- Architecture: Determining the amount of material needed for circular designs or structures.
- Mathematics: Solving complex geometrical problems involving circles.
- Everyday Life: Estimating the size of circular objects like pizzas, ponds, or roundabouts.
2. Calculating the Area of a Circle Using Radius
The most straightforward method to find the area of a circle is by using its radius. The formula is simple and widely applicable, making it a fundamental skill for students and professionals alike.
2.1. The Formula for Area Using Radius
The formula to calculate the area (A) of a circle using its radius (r) is:
A = πr²
Where:
- A is the area of the circle.
- π (pi) is approximately 3.14159.
- r is the radius of the circle.
2.2. Step-by-Step Calculation
To calculate the area of a circle using the radius, follow these steps:
- Identify the Radius: Determine the length of the radius (r).
- Square the Radius: Multiply the radius by itself (r²).
- Multiply by Pi: Multiply the result by π (approximately 3.14159).
For example, if a circle has a radius of 5 meters, the calculation would be:
A = π (5m)²
A = 3.14159 25m²
A ≈ 78.54 m²
2.3. Example Problems
Let’s work through a few more examples to solidify your understanding:
-
Example 1: A circle has a radius of 10 cm. Find its area.
- A = π * (10cm)²
- A = 3.14159 * 100cm²
- A ≈ 314.16 cm²
-
Example 2: A circle has a radius of 3 inches. Find its area.
- A = π * (3in)²
- A = 3.14159 * 9in²
- A ≈ 28.27 in²
2.4. Common Mistakes to Avoid
When calculating the area of a circle using the radius, avoid these common mistakes:
- Forgetting to Square the Radius: Always remember to square the radius before multiplying by π.
- Using Diameter Instead of Radius: If you are given the diameter, make sure to divide it by 2 to get the radius.
- Rounding Errors: Use enough decimal places for π to maintain accuracy, especially in precise calculations.
3. Calculating the Area of a Circle Using Diameter
If you know the diameter of a circle, you can still easily find its area. The diameter is simply twice the radius, so a slight modification of the formula is all you need.
3.1. The Formula for Area Using Diameter
The formula to calculate the area (A) of a circle using its diameter (d) is:
A = π (d/2)²
Or, simplified:
A = (π/4) d²
Where:
- A is the area of the circle.
- π (pi) is approximately 3.14159.
- d is the diameter of the circle.
3.2. Step-by-Step Calculation
To calculate the area of a circle using the diameter, follow these steps:
- Identify the Diameter: Determine the length of the diameter (d).
- Divide by Two: Divide the diameter by 2 to get the radius (r = d/2).
- Square the Result: Square the result from step 2 ((d/2)²).
- Multiply by Pi: Multiply the result by π (approximately 3.14159).
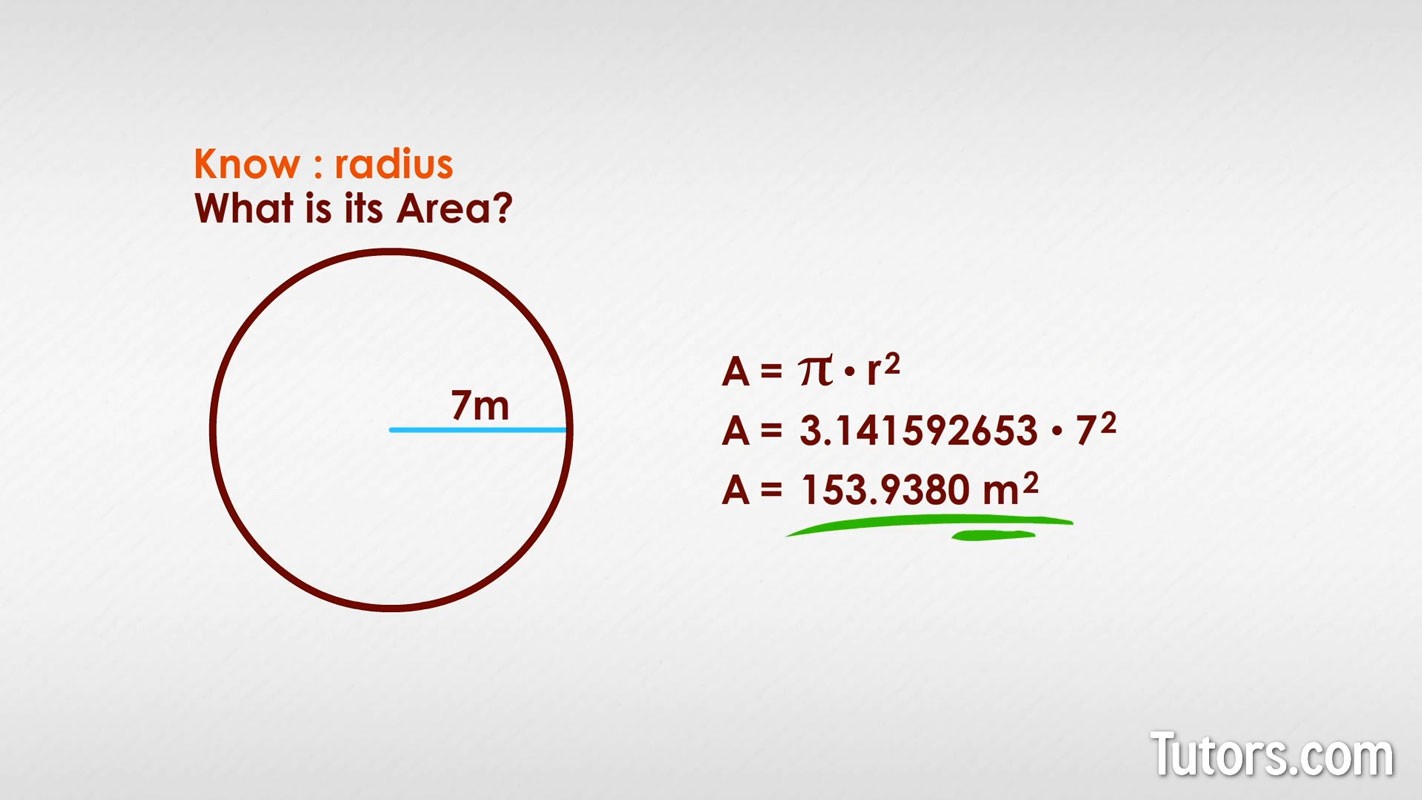
For example, if a circle has a diameter of 14 meters, the calculation would be:
A = π (14m/2)²
A = π (7m)²
A = 3.14159 * 49m²
A ≈ 153.94 m²
3.3. Example Problems
Let’s work through a few more examples to ensure you’ve got a handle on it:
-
Example 1: A circle has a diameter of 20 cm. Find its area.
- A = π * (20cm/2)²
- A = π * (10cm)²
- A = 3.14159 * 100cm²
- A ≈ 314.16 cm²
-
Example 2: A circle has a diameter of 6 inches. Find its area.
- A = π * (6in/2)²
- A = π * (3in)²
- A = 3.14159 * 9in²
- A ≈ 28.27 in²
3.4. Real-World Application: Area of a Circular Garden
Consider a circular garden with a diameter of 8 meters. To find the area of the garden:
A = π (8m/2)²
A = π (4m)²
A = 3.14159 * 16m²
A ≈ 50.27 m²
This means you would need approximately 50.27 square meters of soil to cover the garden.
4. Calculating the Area of a Circle Using Circumference
Sometimes, instead of the radius or diameter, you might only know the circumference of a circle. In such cases, you can still calculate the area using a derived formula.
4.1. The Formula for Area Using Circumference
The formula to calculate the area (A) of a circle using its circumference (C) is derived from the relationships A = πr² and C = 2πr. Solving for r in the circumference formula gives r = C / (2π). Substituting this into the area formula gives:
A = π * (C / (2π))²
A = C² / (4π)
Where:
- A is the area of the circle.
- π (pi) is approximately 3.14159.
- C is the circumference of the circle.
4.2. Step-by-Step Calculation
To calculate the area of a circle using the circumference, follow these steps:
- Identify the Circumference: Determine the length of the circumference (C).
- Square the Circumference: Multiply the circumference by itself (C²).
- Divide by 4π: Divide the result by 4π (4 * 3.14159 ≈ 12.56636).
For example, if a circle has a circumference of 25 meters, the calculation would be:
A = (25m)² / (4 * π)
A = 625m² / 12.56636
A ≈ 49.74 m²
4.3. Example Problems
Let’s go through a couple more examples to make sure you understand the calculation:
-
Example 1: A circle has a circumference of 30 cm. Find its area.
- A = (30cm)² / (4 * π)
- A = 900cm² / 12.56636
- A ≈ 71.62 cm²
-
Example 2: A circle has a circumference of 10 inches. Find its area.
- A = (10in)² / (4 * π)
- A = 100in² / 12.56636
- A ≈ 7.96 in²
4.4. Practical Scenario: Designing a Circular Patio
Suppose you’re designing a circular patio and you know the total length of the paving stones you have available (the circumference) is 40 meters. To find the area of the patio:
A = (40m)² / (4 * π)
A = 1600m² / 12.56636
A ≈ 127.32 m²
This helps you determine if the area is suitable for your needs.
5. Advanced Applications and Considerations
While the basic formulas cover most scenarios, there are advanced applications and considerations that can further enhance your understanding and precision in calculating the area of a circle.
5.1. Using Pi (π) with Higher Precision
For most practical purposes, using π ≈ 3.14159 is sufficient. However, in fields like engineering and physics, where precision is critical, using a more precise value of π is necessary. Many calculators and software programs provide π to many decimal places. Using a higher precision value can significantly affect the accuracy of your calculations, especially for large circles.
5.2. Calculating the Area of a Sector of a Circle
A sector of a circle is a portion of the circle enclosed by two radii and an arc. To find the area of a sector, you need to know the radius (r) and the angle (θ) in degrees or radians subtended by the arc at the center.
If the angle is in degrees, the area of the sector is given by:
A_sector = (θ / 360) * πr²
If the angle is in radians, the area of the sector is given by:
A_sector = (θ / 2) * r²
For example, if a circle has a radius of 8 cm and a sector with an angle of 45 degrees, the area of the sector would be:
A_sector = (45 / 360) π (8cm)²
A_sector = (1/8) 3.14159 64cm²
A_sector ≈ 25.13 cm²
5.3. Calculating the Area of a Circular Segment
A circular segment is the region bounded by an arc and a chord (a straight line connecting the endpoints of the arc). To find the area of a segment, you first find the area of the sector and then subtract the area of the triangle formed by the radii and the chord.
The formula to calculate the area of a segment is:
A_segment = (r² / 2) * (θ – sin(θ))
Where:
- r is the radius of the circle.
- θ is the angle in radians.
5.4. Practical Tips for Accurate Calculations
To ensure accurate calculations, consider these tips:
- Use Consistent Units: Make sure all measurements are in the same units (e.g., meters, centimeters, inches) before performing calculations.
- Double-Check Your Work: Always review your calculations to avoid simple arithmetic errors.
- Use a Calculator: Utilize a calculator with a π button for more accurate results.
- Consider Significant Figures: Pay attention to significant figures, especially in scientific and engineering applications, to maintain precision.
6. Real-Life Applications of Circle Area Calculations
Calculating the area of a circle is not just a theoretical exercise; it has numerous practical applications in various fields.
6.1. Engineering and Construction
In engineering, calculating the area of circles is crucial for designing various structures. For example:
- Pipes and Cylinders: Determining the cross-sectional area of pipes to calculate flow rates.
- Circular Foundations: Estimating the amount of concrete needed for circular foundations of buildings.
- Tunnels: Calculating the area of tunnel cross-sections for ventilation and structural integrity.
6.2. Architecture and Design
Architects and designers often need to calculate the area of circular elements in their designs. This includes:
- Circular Rooms: Determining the flooring or roofing materials needed for circular rooms.
- Round Windows: Calculating the glass area for round windows.
- Landscaping: Planning circular gardens, fountains, or ponds.
6.3. Manufacturing and Production
In manufacturing, calculating the area of circles is essential for:
- Cutting Materials: Estimating the amount of material needed to cut out circular shapes from sheets of metal, fabric, or paper.
- Product Design: Designing circular components for machines and devices.
- Packaging: Calculating the surface area of circular packaging containers.
6.4. Science and Research
Scientists use circle area calculations in various research fields:
- Astronomy: Calculating the area of celestial bodies or orbits.
- Physics: Determining the cross-sectional area of particles or beams.
- Biology: Estimating the area of circular cells or Petri dishes.
7. Common Questions About Finding the Area of a Circle (FAQ)
To help you further understand the topic, here are some frequently asked questions about finding the area of a circle.
7.1. What is the formula for the area of a circle?
The formula for the area (A) of a circle is A = πr², where r is the radius of the circle and π (pi) is approximately 3.14159.
7.2. How do I find the area of a circle if I only know the diameter?
If you know the diameter (d) of the circle, divide it by 2 to find the radius (r = d/2) and then use the formula A = πr². Alternatively, you can use the formula A = (π/4) * d².
7.3. How do I find the area of a circle if I only know the circumference?
If you know the circumference (C) of the circle, use the formula A = C² / (4π) to find the area.
7.4. Why is pi (π) important in calculating the area of a circle?
Pi (π) is a mathematical constant that represents the ratio of a circle’s circumference to its diameter. It is essential for calculating the area because it relates the radius (or diameter) to the space enclosed within the circle.
7.5. Can I use any value for pi (π) or should I use a specific one?
While π is an irrational number with infinite decimal places, using π ≈ 3.14159 is generally sufficient for most calculations. However, for more precise calculations, you can use a calculator or software that provides π to more decimal places.
7.6. What are the units for the area of a circle?
The units for the area of a circle are square units, such as square meters (m²), square centimeters (cm²), square inches (in²), or square feet (ft²), depending on the units used for the radius or diameter.
7.7. How do I calculate the area of a semi-circle or quarter-circle?
To calculate the area of a semi-circle (half-circle), find the area of the full circle and divide it by 2. To calculate the area of a quarter-circle, find the area of the full circle and divide it by 4.
7.8. What is a sector of a circle, and how do I find its area?
A sector of a circle is a portion of the circle enclosed by two radii and an arc. The area of a sector can be found using the formula A_sector = (θ / 360) * πr², where θ is the angle in degrees subtended by the arc at the center.
7.9. How does the area of a circle relate to its perimeter (circumference)?
The area of a circle (A) is related to its circumference (C) by the formula A = C² / (4π). This relationship allows you to calculate the area if you only know the circumference, and vice versa.
7.10. Are there any online tools or calculators to help find the area of a circle?
Yes, there are many online tools and calculators available that can help you find the area of a circle. These tools typically require you to input the radius, diameter, or circumference, and they will calculate the area for you.
8. The Expertise of HOW.EDU.VN: Circle Area and Beyond
At HOW.EDU.VN, we understand the importance of accuracy and clarity in mathematical calculations. Our team of expert Doctors and specialists are dedicated to providing top-notch guidance and support in various fields, including mathematics, engineering, and architecture. With years of experience and a commitment to excellence, we ensure that you receive the most reliable and practical advice.
8.1. Meet Our Experts
| Field | Expert Name | Expertise |
|---|---|---|
| Mathematics | Dr. Emily Carter | Geometry, Calculus, Mathematical Modeling |
| Engineering | Dr. James Wilson | Structural Engineering, Fluid Dynamics, Thermodynamics |
| Architecture | Dr. Sarah Johnson | Sustainable Design, Urban Planning, Architectural Theory |
| Science | Dr. Michael Davis | Astronomy, Physics, Biology |
8.2. How HOW.EDU.VN Can Help You
Navigating complex calculations like finding the area of a circle requires expertise. Here’s how HOW.EDU.VN can assist you:
- Personalized Consultations: Connect with our expert Doctors for tailored advice and solutions.
- Detailed Explanations: Gain a deeper understanding of circle area and related mathematical concepts with our comprehensive resources.
- Practical Problem-Solving: Learn how to apply circle area calculations in real-world scenarios and projects.
- Step-by-Step Guidance: Follow our clear, step-by-step instructions for accurate calculations.
- Advanced Insights: Explore advanced applications and considerations for professionals and enthusiasts.
9. Take the Next Step with HOW.EDU.VN
Calculating the area of a circle is a foundational skill with wide-ranging applications. Whether you’re a student, professional, or simply curious, mastering this concept will undoubtedly be valuable. At HOW.EDU.VN, we are committed to providing you with the expertise and resources you need to excel. Don’t let complex calculations intimidate you; let our team of experienced Doctors guide you to success.
9.1. Connect with Our Experts Today
Ready to take your understanding of circle area to the next level? Contact our expert Doctors at HOW.EDU.VN for personalized consultations and detailed solutions. Whether you’re facing challenges in engineering, architecture, or any other field, we have the knowledge and experience to help you succeed. Reach out to us today and experience the difference that expert guidance can make.
9.2. Why Choose HOW.EDU.VN?
- Expert Doctors: Access a network of over 100 renowned Doctors specializing in various fields.
- Personalized Support: Receive customized advice tailored to your specific needs and challenges.
- Reliable Information: Trust in our commitment to accuracy and clarity.
- Comprehensive Resources: Benefit from our extensive collection of articles, guides, and tutorials.
- Real-World Solutions: Learn how to apply your knowledge in practical scenarios and projects.
Don’t hesitate to reach out to us. Your success is our priority.
Contact Information:
Address: 456 Expertise Plaza, Consult City, CA 90210, United States
WhatsApp: +1 (310) 555-1212
Website: HOW.EDU.VN
Let HOW.EDU.VN be your trusted partner in mastering circle area calculations and achieving your goals. Connect with us today and discover the power of expert guidance.
 Bicycle Wheel Area Calculation
Bicycle Wheel Area Calculation
10. Call to Action: Get Expert Advice Now
Do you find yourself struggling with complex calculations or seeking advice on a project that requires precise area determination? Don’t waste time and resources on guesswork. The expertise of HOW.EDU.VN is at your fingertips.
Our team of Doctors and specialists is ready to provide you with the personalized support and detailed solutions you need to achieve your goals.
Here’s what you can gain from connecting with us:
- Confidence: Ensure your calculations are accurate and reliable with expert guidance.
- Efficiency: Save time and resources by avoiding costly errors and rework.
- Innovation: Unlock new possibilities and creative solutions with expert insights.
- Success: Achieve your goals with the support of experienced professionals.
Ready to experience the difference expert guidance can make?
Contact HOW.EDU.VN today and let us help you transform your challenges into opportunities. Visit our website at HOW.EDU.VN or reach out to us via WhatsApp at +1 (310) 555-1212. Our team is available to answer your questions and provide you with the tailored solutions you need.
Don’t wait any longer. Your success starts now with HOW.EDU.VN. We are more than just a website; we are your partners in progress. Join the countless others who have benefited from our expertise and experience the difference that personalized support can make.
Let how.edu.vn be your guiding star in the world of complex calculations and innovative solutions. Contact us today and let’s work together towards your success.
