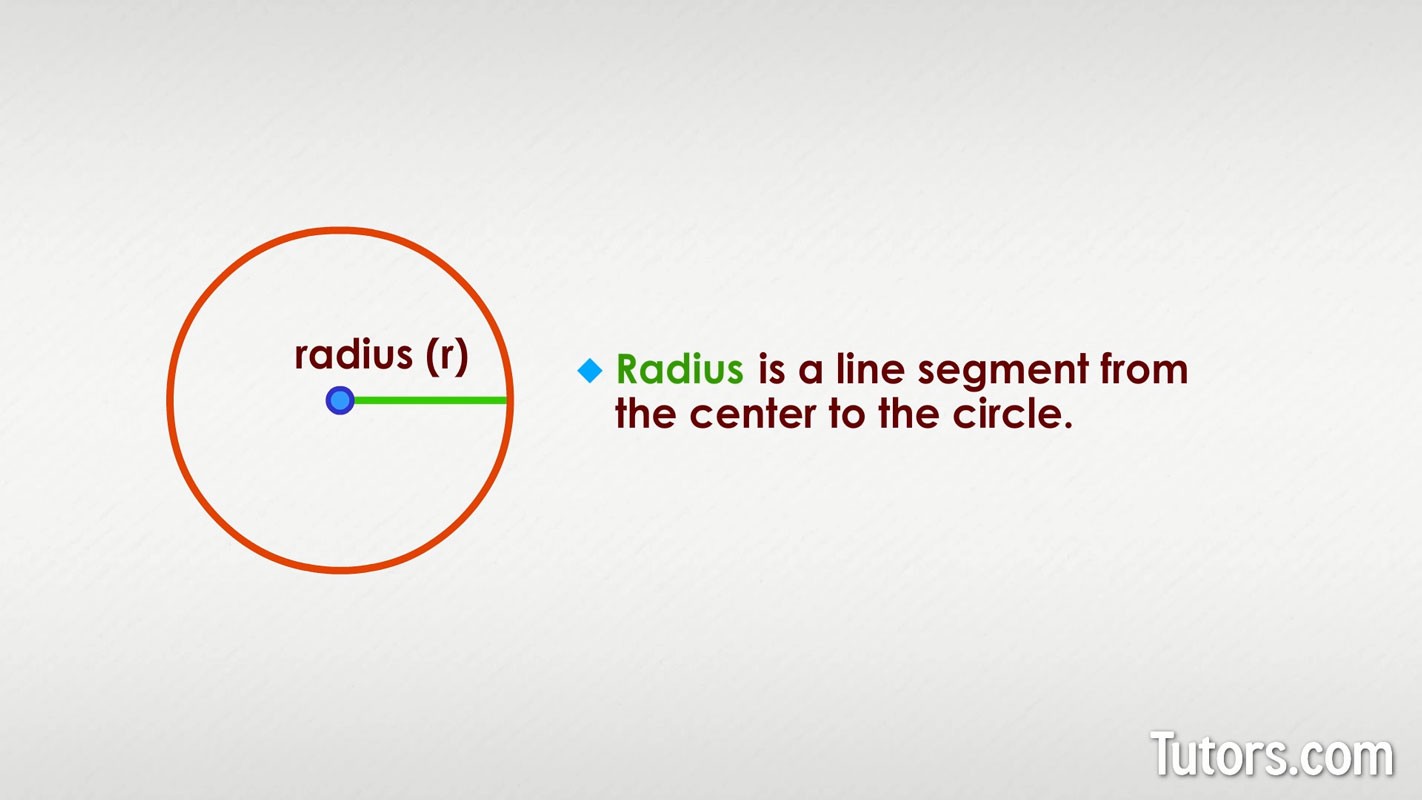
In geometry, the radius of a circle is a fundamental measurement that defines its size. It’s the distance from the center of the circle to any point on its circumference. Represented by the lowercase italic letter r, understanding how to find the radius is crucial for solving various geometrical problems and real-world applications.
Whether you’re a student tackling homework, a DIY enthusiast working on a project, or simply curious about circles, knowing how to calculate the radius is a valuable skill. This guide will walk you through different methods and formulas to easily determine the radius of a circle based on the information you have available, be it the circumference, area, or diameter.
Understanding the Radius of a Circle
Before diving into calculations, let’s solidify our understanding of what the radius is. Imagine a circle as a wheel. The radius is like a spoke extending from the very center of the wheel to its outer edge. Every spoke in that wheel, regardless of where it’s placed around the circle, will be the same length – this is the defining characteristic of the radius.
Radius of a circle definition, showing a line from the center to the edge
The radius is intrinsically linked to another key measurement of a circle: the diameter. The diameter (d) is a straight line passing through the center of the circle, connecting two points on opposite sides of the circumference. As you can see in the image above, the diameter essentially cuts the circle in half through its center. This relationship is key to one of the simplest methods of finding the radius.
Methods to Calculate the Radius
The beauty of geometry lies in its interconnectedness. Depending on what information you have about a circle, you can use different formulas to find its radius. Let’s explore the most common scenarios:
1. Finding the Radius from the Diameter
This is the most straightforward method. As we touched upon earlier, the diameter is twice the length of the radius. Therefore, to find the radius when you know the diameter, you simply divide the diameter by 2.
Formula:
r = d / 2
Where:
- r = radius
- d = diameter
Example:
If you have a circle with a diameter of 10 inches, you can find the radius as follows:
r = 10 inches / 2 = 5 inches
Thus, the radius of the circle is 5 inches.
Instructional image showing diameter being divided by two to find radius
Conversely, if you know the radius and need to find the diameter, you would multiply the radius by 2 (d = 2r).
2. Finding the Radius from the Circumference
The circumference (C) of a circle is the distance around it – essentially, its perimeter. The relationship between the circumference and the radius is defined by the mathematical constant pi (π), which is approximately 3.14159.
The formula for the circumference of a circle is: C = 2πr
To find the radius when you know the circumference, you need to rearrange this formula to solve for r. Dividing both sides of the equation by 2π isolates r:
Formula:
r = C / (2π)
Where:
- r = radius
- C = circumference
- π (pi) ≈ 3.14159
Example:
Suppose you have a circle with a circumference of 25 centimeters. To find the radius:
r = 25 cm / (2 π)
r ≈ 25 cm / (2 3.14159)
r ≈ 25 cm / 6.28318
r ≈ 3.98 cm
Therefore, the radius of the circle is approximately 3.98 centimeters.
Visual representation showing circumference formula rearranged to find radius
3. Finding the Radius from the Area
The area (A) of a circle is the space it occupies within its circumference, measured in square units. The formula for the area of a circle is: A = πr²
To find the radius when you know the area, you need to rearrange this formula to solve for r. This involves taking the square root.
Formula:
r = √(A / π)
Where:
- r = radius
- A = area
- π (pi) ≈ 3.14159
- √ indicates the square root
Example:
Let’s say you have a circle with an area of 50 square meters. To calculate the radius:
r = √(50 sq meters / π)
r ≈ √(50 sq meters / 3.14159)
r ≈ √(15.915 sq meters)
r ≈ 3.99 meters
Thus, the radius of the circle is approximately 3.99 meters.
Diagram illustrating the area formula being manipulated to solve for radius
Radius Formulas at a Glance
To summarize, here are the formulas you can use to find the radius of a circle depending on the given information:
Summary image showing three formulas to calculate circle radius from diameter, circumference, and area
- From Diameter (d): r = d / 2
- From Circumference (C): r = C / (2π)
- From Area (A): r = √(A / π)
Practice Examples
Let’s test your understanding with a few examples:
- A circle has a diameter of 14 cm. What is its radius?
- A circle has a circumference of 44 inches. What is its radius? (Use π ≈ 22/7)
- A circle has an area of 113.1 square feet. What is its radius? (Use π ≈ 3.14)
Answers:
- Radius = 14 cm / 2 = 7 cm
- Radius = 44 inches / (2 * 22/7) = 44 inches / (44/7) = 7 inches
- Radius = √(113.1 sq ft / 3.14) = √(36 sq ft) = 6 feet
Conclusion
Understanding how to find the radius of a circle is a fundamental skill in geometry with practical applications in various fields. By mastering these formulas and methods, you can confidently solve problems involving circles, whether you are working with diameter, circumference, or area. Remember to choose the appropriate formula based on the information provided, and you’ll be able to calculate the radius of any circle with ease.