Understanding how to calculate the area of a rectangle is a fundamental concept in geometry and has practical applications in everyday life. Whether you’re figuring out how much carpet to buy for a room, calculating the size of a garden plot, or working on a math problem, knowing How To Find The Area Of A Rectangle is essential. In simple terms, the area of a rectangle is the amount of space it occupies within its boundaries. This guide will walk you through everything you need to know, from the basic formula to more advanced methods and real-world examples.
What is the Area of a Rectangle?
In geometry, area refers to the two-dimensional space enclosed within a shape. When we talk about the area of a rectangle, we are referring to the amount of surface covered by the rectangle. Imagine covering a rectangular floor with square tiles; the area is essentially the number of tiles needed to cover the entire floor without any gaps or overlaps.
Formally, the area of a rectangle is defined as the number of unit squares that can fit perfectly within the rectangle. A “unit square” is a square with sides of length 1 unit (e.g., 1 inch, 1 centimeter, 1 foot). Therefore, the area is always expressed in square units such as square inches, square centimeters, square feet, etc.
Rectangular shapes are all around us. Think about everyday objects like:
- Smartphone screens: The display area you interact with.
- Tabletops: The flat surface where you place items.
- Book covers: The front and back surfaces of a book.
- Fields and gardens: Often designed in rectangular plots for efficient use of space.
Understanding how to calculate the area of a rectangle allows us to quantify the size of these surfaces and solve a variety of practical problems.
Visual representation of the area of a rectangle. This image illustrates how unit squares fit within a rectangle to define its area, a key concept in understanding how to find the area of a rectangle.
The Area of a Rectangle Formula
The most straightforward way to find the area of a rectangle is by using a simple formula. This formula directly relates the area to the rectangle’s dimensions: its length and width.
The formula for the area of a rectangle is:
Area = Length × Width
Or, in symbolic form:
A = l × w
Where:
- A represents the Area of the rectangle.
- l represents the Length of the rectangle (the longer side).
- w represents the Width of the rectangle (the shorter side, sometimes also called breadth).
To use this formula, you simply need to know the length and width of the rectangle. Make sure that both dimensions are in the same units before you multiply them. The result will be the area in square units of the same unit of measurement.
Step-by-Step Guide: How to Calculate the Area of a Rectangle
Calculating the area of a rectangle using the formula is a simple three-step process:
Step 1: Identify the Length and Width
First, determine the length and width of the rectangle. These dimensions will usually be given in the problem statement or can be measured directly if you are dealing with a real-world object. Ensure that both length and width are in the same units (e.g., inches, feet, meters, centimeters). If they are not, you’ll need to convert one of them to match the other’s unit.
Step 2: Multiply Length by Width
Next, multiply the length and width values together. This is a straightforward multiplication operation.
Step 3: State the Area in Square Units
Finally, express your answer in square units. If the length and width were in inches, the area will be in square inches (in²). If they were in centimeters, the area will be in square centimeters (cm²), and so on. Always remember to include the square unit in your final answer to correctly represent area.
Example:
Let’s find the area of a rectangle with a length of 12 centimeters and a width of 5 centimeters.
- Length (l) = 12 cm, Width (w) = 5 cm
- Area = Length × Width = 12 cm × 5 cm = 60
- Area = 60 cm² (square centimeters)
Therefore, the area of the rectangle is 60 square centimeters.
Understanding Square Units in Area Calculation
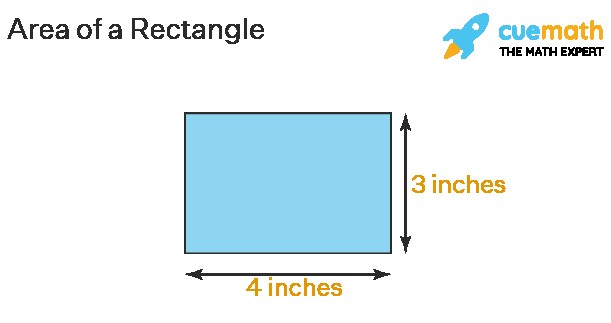
Why is the area expressed in square units? Let’s visualize this with an example. Imagine a rectangle that is 4 inches long and 3 inches wide.
If you were to draw this rectangle and divide it into a grid of 1-inch squares, you would find that you can fit exactly 12 of these squares inside the rectangle. Each of these squares is a “square inch” (1 inch × 1 inch). The total number of these 1-inch squares that fit within the rectangle is its area.
Visual representation of square units illustrating area. This image shows a rectangle divided into square units, emphasizing why area is measured in square units when learning how to find the area of a rectangle.
This concept applies to any unit of measurement. If you are working in centimeters, the area will be in square centimeters, representing the number of 1 cm × 1 cm squares that fit in the shape. This fundamental idea explains why area is always measured in square units, reinforcing the concept of how to find the area of a rectangle.
Finding the Area of a Rectangle Using the Diagonal
Sometimes, instead of the length and width, you might be given the diagonal of a rectangle and one of its sides. The diagonal of a rectangle is a line segment that connects opposite corners. We can still find the area in such cases by using the Pythagorean theorem.
A rectangle’s diagonal divides it into two right-angled triangles. The diagonal acts as the hypotenuse, and the length and width are the two legs of the right triangle. According to the Pythagorean theorem:
Diagonal² = Length² + Width²
We can rearrange this formula to find a missing side if we know the diagonal and the other side.
Method 1: Using the Pythagorean Theorem to Find a Missing Side
- Identify the knowns: You know the diagonal (d) and one side (let’s say length, l). You need to find the width (w).
- Use the Pythagorean theorem to solve for the unknown side: Rearrange the theorem to solve for width:
Width² = Diagonal² – Length²
Width = √(Diagonal² – Length²) - Calculate the Width.
- Use the area formula: Once you have the width, use the standard area formula: Area = Length × Width.
Example:
Find the area of a rectangle with a length of 8 cm and a diagonal of 10 cm.
- Diagonal (d) = 10 cm, Length (l) = 8 cm, Width (w) = ?
- Width = √(Diagonal² – Length²) = √(10² – 8²) = √(100 – 64) = √36 = 6 cm
- Width = 6 cm
- Area = Length × Width = 8 cm × 6 cm = 48 cm²
Thus, the area of the rectangle is 48 square centimeters.
Method 2: Direct Formula (Less Common but Possible)
You can also derive a formula to directly calculate the area if you know the diagonal and one side, though it’s less commonly used and understanding the Pythagorean approach is generally more beneficial. For example, if you know the diagonal (d) and the width (w), you can express the length as:
Length = √(Diagonal² – Width²)
And substitute this into the area formula:
Area = √(Diagonal² – Width²) × Width
Or if you know the diagonal (d) and the length (l):
Area = Length × √(Diagonal² – Length²)
These formulas are derived directly from using the Pythagorean theorem within the area formula, providing an alternative method on how to find the area of a rectangle when given the diagonal.
Finding the Area of a Rectangle Using the Perimeter
Another scenario is when you are given the perimeter of a rectangle and one of its sides. The perimeter is the total distance around the rectangle, calculated by adding up the lengths of all four sides. The formula for the perimeter of a rectangle is:
Perimeter = 2 × (Length + Width)
If you know the perimeter and one side, you can find the other side and then calculate the area.
Steps to find the area using perimeter:
- Identify the knowns: You know the Perimeter (P) and one side (let’s say length, l). You need to find the width (w).
- Use the perimeter formula to solve for the unknown side:
Perimeter = 2 × (Length + Width)
P = 2l + 2w
P – 2l = 2w
Width = (P – 2l) / 2 - Calculate the Width.
- Use the area formula: Once you have the width, use the standard area formula: Area = Length × Width.
Example:
Find the area of a rectangle with a perimeter of 30 units and a length of 9 units.
- Perimeter (P) = 30 units, Length (l) = 9 units, Width (w) = ?
- Width = (P – 2l) / 2 = (30 – 2 × 9) / 2 = (30 – 18) / 2 = 12 / 2 = 6 units
- Width = 6 units
- Area = Length × Width = 9 units × 6 units = 54 square units
Therefore, the area of the rectangle is 54 square units.
Derivation of the Area of a Rectangle Formula
The formula for the area of a rectangle can be intuitively understood and also geometrically derived. Consider a rectangle ABCD. Draw a diagonal AC. This diagonal divides the rectangle into two congruent right-angled triangles, ΔABC and ΔADC.
Derivation of the area of a rectangle formula. This image illustrates how a rectangle is divided into two triangles to derive the area formula, providing a visual aid to understanding how to find the area of a rectangle.
The area of the rectangle is the sum of the areas of these two triangles:
Area of Rectangle ABCD = Area of ΔABC + Area of ΔADC
Since ΔABC and ΔADC are congruent, they have equal areas. So,
Area of Rectangle ABCD = 2 × Area of ΔABC
The area of a triangle is given by: Area of Triangle = (1/2) × Base × Height. In triangle ΔABC, the base is AB (length) and the height is BC (width).
Area of ΔABC = (1/2) × AB × BC
Substituting this back into the equation for the rectangle’s area:
Area of Rectangle ABCD = 2 × [(1/2) × AB × BC]
Area of Rectangle ABCD = AB × BC
Therefore, Area of Rectangle = Length × Width, which is the formula we use. This derivation shows how the area formula is rooted in more fundamental geometric principles, further clarifying how to find the area of a rectangle.
Real-World Examples of Calculating Rectangle Area
Let’s look at some practical examples of how to use the area of a rectangle formula in real-life situations:
Example 1: Calculating the Area of a Farm
A farmer has a rectangular farm that is 150 yards long and 80 yards wide. What is the area of the farm?
- Length = 150 yards
- Width = 80 yards
- Area = Length × Width = 150 yards × 80 yards = 12,000 square yards
The area of the farm is 12,000 square yards.
Example 2: Finding the Area of a Tabletop
A rectangular tabletop measures 48 inches in length and 24 inches in width. Calculate the area of the tabletop.
- Length = 48 inches
- Width = 24 inches
- Area = Length × Width = 48 inches × 24 inches = 1,152 square inches
The area of the tabletop is 1,152 square inches.
Example 3: Area Calculation with Decimal Dimensions
What is the area of a rectangular piece of paper that is 8.5 inches long and 11 inches wide?
- Length = 11 inches
- Width = 8.5 inches
- Area = Length × Width = 11 inches × 8.5 inches = 93.5 square inches
The area of the paper is 93.5 square inches.
Practice Questions on Area of Rectangle
Test your understanding with these practice questions:
- A rectangle has a length of 20 cm and a width of 15 cm. What is its area?
- The area of a rectangular garden is 300 square feet. If the width of the garden is 15 feet, what is its length?
- A rectangular banner is 5 feet long and 2 feet wide. How much material is needed to make the banner?
- Which rectangle has a larger area: one with dimensions 7m x 5m or another with dimensions 8m x 4m?
- Calculate the area of a rectangular floor that measures 12 feet by 15 feet.
Frequently Asked Questions (FAQs) About the Area of a Rectangle
Q1: What is the area of a rectangle in geometry?
A: In geometry, the area of a rectangle is the region enclosed within its four sides. It’s the measure of the surface covered by the rectangle and is found by multiplying its length and width. The area is always expressed in square units.
Q2: What are perimeter and area, and how do they differ for a rectangle?
A: The perimeter of a rectangle is the total length of its boundary, found by adding up all four sides, or using the formula Perimeter = 2 × (Length + Width). It’s a measure of distance around the shape and is expressed in linear units (like inches, meters). The area, on the other hand, is the space enclosed within the rectangle, calculated as Area = Length × Width. Area is a measure of surface and is expressed in square units (like square inches, square meters). Perimeter measures the distance around, while area measures the surface inside.
Q3: What is the standard formula for the area of a rectangle?
A: The standard formula for calculating the area of a rectangle is: Area = Length × Width or A = l × w.
Q4: What are the units of measurement for the area of a rectangle?
A: The area of a rectangle is always measured in square units. If the dimensions (length and width) are given in inches, the area will be in square inches (in²). If the dimensions are in centimeters, the area will be in square centimeters (cm²), and so on. Square units reflect the two-dimensional nature of area.
Q5: How can I find the area of a rectangle if I know the diagonal and one side?
A: If you know the diagonal and one side (either length or width), you can use the Pythagorean theorem to find the missing side. If you know the diagonal (d) and length (l), then Width = √(d² – l²). Once you find the width, you can use the area formula: Area = Length × Width.
Q6: What defines a rectangle in geometry?
A: A rectangle is a quadrilateral (a four-sided closed shape) with four right angles (90°). Its opposite sides are equal in length and parallel. Squares are special types of rectangles where all four sides are equal.
Q7: How do I calculate the area of a rectangle when the dimensions are given as fractions or mixed numbers?
A: The method is the same: multiply the length by the width. If you have fractions, multiply them as you would any fractions. If you have mixed numbers, first convert them into improper fractions and then multiply. For example, if Length = 2 1/2 inches and Width = 1 1/4 inches, convert to improper fractions: Length = 5/2 inches, Width = 5/4 inches. Then, Area = (5/2) × (5/4) = 25/8 = 3 1/8 square inches.
Q8: How do I find the area of a rectangle when I am given the perimeter and one side?
A: If you know the perimeter (P) and one side (e.g., length, l), you can find the width using the perimeter formula: Width = (P – 2l) / 2. Once you have the width, calculate the area using Area = Length × Width.
Q9: Is the area of a rectangle always smaller than its perimeter?
A: Not always. The relationship between area and perimeter depends on the dimensions of the rectangle. For some rectangles, the area can be numerically larger than the perimeter, especially when the sides are long. For example, a rectangle with length 10 and width 1 has an area of 10 and a perimeter of 22. But a rectangle with length 5 and width 5 (a square) has an area of 25 and a perimeter of 20, in this case, the area is larger.
Q10: Can the area of a rectangle be zero or negative?
A: In practical geometry, the area of a rectangle cannot be zero or negative. Length and width are always positive values, so their product (area) will also always be positive. A zero area would imply a degenerate rectangle with either zero length or zero width, which is not typically considered a rectangle in the standard geometric sense.
This comprehensive guide has covered various methods on how to find the area of a rectangle, from the basic formula to more complex scenarios involving diagonals and perimeters. Understanding these concepts is crucial for both mathematical studies and practical applications in everyday life.