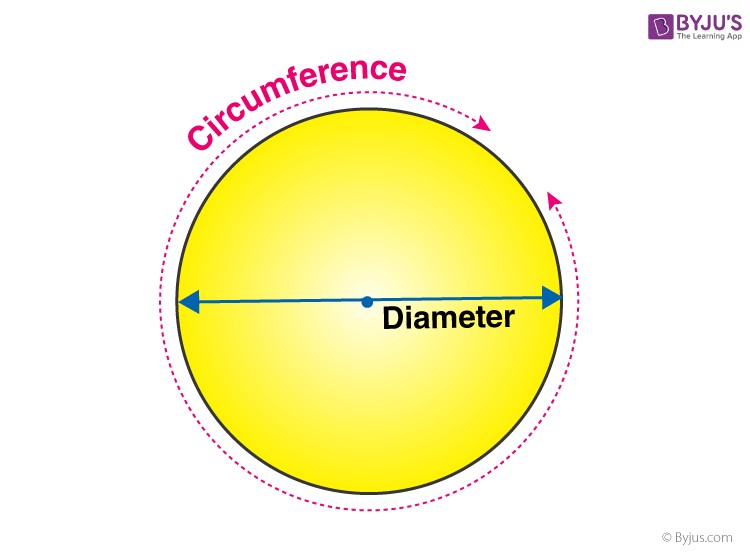
In mathematics, the circumference of a circle is defined as the distance around its edge. You can also think of it as the perimeter of a circle. Understanding how to calculate the circumference is fundamental in geometry and has practical applications in various fields. This article will guide you through the definition, formulas, and methods to accurately find the circumference of any circle.
Understanding Circle Circumference
The circumference of a circle, often referred to as the perimeter of a circle, is essentially the length of the boundary that encloses the circular shape. Imagine unrolling a circle into a straight line; the length of this line would be the circumference. It’s a linear measurement, typically expressed in units like centimeters (cm), meters (m), inches, or feet.
To calculate the circumference, we need to understand the relationship between the circumference and key features of a circle, namely its radius and diameter. The radius of a circle is the distance from the center of the circle to any point on its edge. The diameter of a circle is a straight line passing through the center and connecting two points on the circle’s edge. The diameter is always twice the length of the radius.
Formulas for Calculating Circumference
There are two primary formulas to calculate the circumference of a circle, depending on whether you know the radius or the diameter. Both formulas utilize a mathematical constant called Pi (π), which is approximately 3.14159. For most calculations, using 3.14 or 22/7 as approximations for π is sufficient.
Formula 1: Using the Radius
If you know the radius (r) of the circle, the formula for the circumference (C) is:
C = 2πr
Where:
- C = Circumference
- π (Pi) ≈ 3.14159
- r = Radius of the circle
Formula 2: Using the Diameter
If you know the diameter (d) of the circle, the formula for the circumference (C) is:
C = πd
Where:
- C = Circumference
- π (Pi) ≈ 3.14159
- d = Diameter of the circle
This second formula is derived from the first one because the diameter is twice the radius (d = 2r). Therefore, substituting 2r for d in C = πd gives C = π(2r) = 2πr, which is the first formula.
Example:
Let’s say a circle has a radius of 5 cm. To find its circumference using Formula 1:
C = 2πr
C = 2 3.14 5
C = 31.4 cm
So, the circumference of the circle is approximately 31.4 cm.
Methods to Find the Circumference
Besides using formulas, there are practical methods to understand and even measure the circumference of a circle.
Method 1: Calculation using Formulas
As discussed above, using the formulas C = 2πr or C = πd is the most accurate method to find the circumference. You simply need to know either the radius or the diameter of the circle and apply the appropriate formula.
Method 2: Measurement (Approximation)
While not as precise as formulas, you can approximate the circumference by physically measuring it. Here’s how you can do it:
- Use a Thread or String: Place a thread or string along the edge of the circle, carefully tracing its boundary.
- Mark and Measure: Mark the point on the thread where it completes one full circle around the object. Then, straighten the thread and measure the distance between the starting point and the marked point using a ruler or measuring tape. This length will be an approximation of the circle’s circumference.
This method is useful for understanding the concept of circumference and for situations where you might not know the radius or diameter but have the physical circle available. However, it’s less accurate than using formulas due to the potential for slight inaccuracies in tracing and measuring.
Solved Examples
Let’s work through some examples to solidify your understanding of How To Find The Circumference Of A Circle.
Example 1:
A circle has a diameter of 10 inches. Calculate its circumference.
Solution:
Given: Diameter (d) = 10 inches
Using the formula C = πd:
C = π 10
C ≈ 3.14 10
C = 31.4 inches
The circumference of the circle is approximately 31.4 inches.
Example 2:
The radius of a circular garden is 7 meters. What is the distance around the garden?
Solution:
Given: Radius (r) = 7 meters
Using the formula C = 2πr:
C = 2 π 7
C ≈ 2 (22/7) 7 (Using 22/7 as an approximation for π for easier calculation)
C = 44 meters
The distance around the garden (circumference) is approximately 44 meters.
Example 3:
Find the circumference of a circle with a radius of 3.5 cm.
Solution:
Given: Radius (r) = 3.5 cm
Using the formula C = 2πr:
C = 2 π 3.5
C ≈ 2 3.14 3.5
C = 21.98 cm
The circumference of the circle is approximately 21.98 cm.
Example 4: Working Backwards
The circumference of a circle is 62.8 cm. What is its radius?
Solution:
Given: Circumference (C) = 62.8 cm
Using the formula C = 2πr and rearranging to solve for r:
r = C / (2π)
r = 62.8 / (2 * 3.14)
r = 62.8 / 6.28
r = 10 cm
The radius of the circle is 10 cm.
Circumference of a Semicircle
A semicircle is exactly half of a circle. To find the perimeter of a semicircle, we need to consider both the curved arc and the straight diameter line that closes the shape.
The curved arc length of a semicircle is half the circumference of the full circle: (1/2) * 2πr = πr.
The straight diameter line is simply 2r.
Therefore, the perimeter of a semicircle is the sum of the arc length and the diameter:
Perimeter of Semicircle = πr + 2r or Perimeter of Semicircle = r(π + 2)
Conclusion
Understanding how to find the circumference of a circle is a basic yet essential skill in mathematics. Whether you are working on geometry problems, designing circular objects, or solving real-world measurement tasks, knowing these formulas and methods will prove invaluable. Remember, the circumference is simply the distance around the circle, and with the radius or diameter, you can easily calculate it using the formulas C = 2πr or C = πd. Practice these examples and you’ll be well-equipped to find the circumference of any circle you encounter.
Practice Questions
- What is the circumference of a circle with a diameter of 14 cm?
- Calculate the circumference of a circle if its radius is 11 inches.
- If a circle has a circumference of 75.36 meters, what is its diameter?
- Find the perimeter of a semicircle with a radius of 4 cm.
- What is the circumference of a coin with a radius of 1.2 cm?
Frequently Asked Questions (FAQs)
Q1: What is the circumference of a circle?
A: The circumference of a circle is the distance around its outer edge, essentially its perimeter.
Q2: How do you calculate the circumference of a circle?
A: You can calculate it using two formulas: C = 2πr (using radius) or C = πd (using diameter), where π (Pi) is approximately 3.14159.
Q3: How do you find the diameter if you know the circumference?
A: You can rearrange the formula C = πd to solve for diameter: d = C / π.
Q4: What is the circumference of a circle with a radius of 10 inches?
A: Using C = 2πr, C = 2 3.14 10 = 62.8 inches.
Q5: Can you find the circumference if you only know the area of the circle?
A: Yes, you can. First, find the radius using the area formula (A = πr²), then use the radius to calculate the circumference using C = 2πr.
This comprehensive guide should provide you with a solid understanding of how to find the circumference of a circle, along with its related concepts and applications.