How to Find the Domain and Range of a Function: Expert Guide

Finding the domain and range of a function is a fundamental concept in mathematics, essential for understanding the behavior and limitations of functions. At HOW.EDU.VN, we provide expert guidance on navigating complex mathematical challenges. Unlock the secrets to defining function boundaries with our comprehensive guide, offering clarity and precision in your mathematical endeavors, ensuring you grasp the allowable inputs and potential outputs. Explore essential concepts, practical applications, and expert insights for mastering function analysis, leading to a deeper understanding of mathematical relationships and problem-solving strategies; identify function boundaries and allowable values with our expert guidance, enhancing precision and confidence in your mathematical pursuits.

1. Understanding Domain and Range

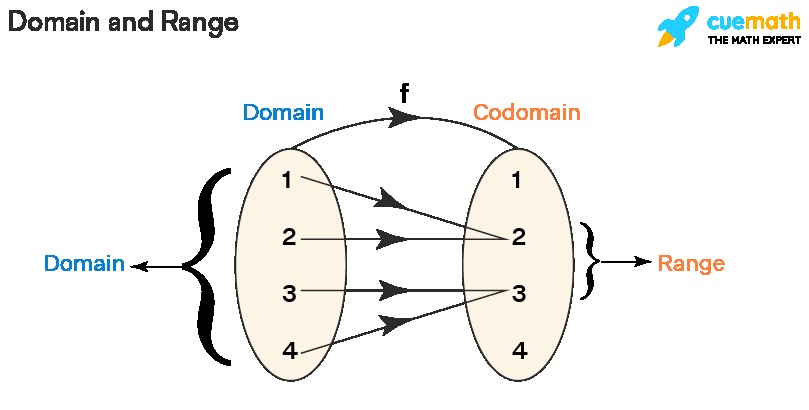
In mathematics, functions are like machines that take an input and produce a unique output. The domain and range define the boundaries of what these machines can accept and produce.

• Domain: The domain of a function is the set of all possible input values (often denoted as ‘x’) for which the function is defined. It represents the values that you can “feed” into the function without causing it to break down (e.g., dividing by zero, taking the square root of a negative number).
• Range: The range of a function is the set of all possible output values (often denoted as ‘y’ or ‘f(x)’) that the function can produce. It represents the values that the function “spits out” after processing the input values from the domain.

Think of a vending machine: the domain is the types of currency the machine accepts, and the range is the selection of products it dispenses.

Understanding the domain and range is crucial for analyzing the behavior of functions, determining their validity, and solving mathematical problems.

2. Importance of Determining Domain and Range

Identifying the domain and range of a function is not merely an academic exercise; it has significant practical implications.

• Real-World Applications: In many real-world scenarios, functions model physical phenomena, and understanding their domain and range ensures that the model remains meaningful and accurate. For instance, a function representing the height of an object can’t have negative values in its range.
• Problem-Solving: Determining the domain and range can help you identify potential issues or limitations in mathematical models, allowing you to refine your approach and arrive at valid solutions.
• Function Analysis: The domain and range provide valuable insights into the behavior of a function, such as its increasing/decreasing intervals, maximum/minimum values, and asymptotes.

3. Strategies for Finding the Domain of a Function

Finding the domain of a function involves identifying any restrictions on the input values that would lead to undefined or invalid results. Here are some common rules and techniques:

3.1. Avoiding Division by Zero

If a function involves a fraction, the denominator cannot be equal to zero. Set the denominator equal to zero and solve for x to find the values that must be excluded from the domain.

Example:

f(x) = 1 / (x - 2)

To find the domain, set the denominator equal to zero:

x - 2 = 0
x = 2

Therefore, the domain is all real numbers except x = 2, which can be written as:

Domain = (-∞, 2) ∪ (2, ∞)

3.2. Dealing with Square Roots

If a function involves a square root, the expression inside the square root must be non-negative (greater than or equal to zero). Set the expression inside the square root greater than or equal to zero and solve for x.

Example:

g(x) = √(x + 3)

To find the domain, set the expression inside the square root greater than or equal to zero:

x + 3 ≥ 0
x ≥ -3

Therefore, the domain is all real numbers greater than or equal to -3, which can be written as:

Domain = [-3, ∞)

3.3. Logarithmic Functions

If a function involves a logarithm, the argument of the logarithm (the expression inside the logarithm) must be positive (greater than zero). Set the argument of the logarithm greater than zero and solve for x.

Example:

h(x) = ln(2x - 1)

To find the domain, set the argument of the logarithm greater than zero:

2x - 1 > 0
2x > 1
x > 1/2

Therefore, the domain is all real numbers greater than 1/2, which can be written as:

Domain = (1/2, ∞)

3.4. Combining Restrictions

Some functions may involve multiple restrictions. In such cases, you need to consider all restrictions and find the intersection of the intervals that satisfy each restriction.

Example:

k(x) = √(x + 2) / (x - 1)

This function has two restrictions:

1. The expression inside the square root must be non-negative: x + 2 ≥ 0 => x ≥ -2
2. The denominator cannot be equal to zero: x - 1 ≠ 0 => x ≠ 1

Combining these restrictions, the domain is all real numbers greater than or equal to -2, except for x = 1, which can be written as:

Domain = [-2, 1) ∪ (1, ∞)

3.5. Polynomial and Exponential Functions

Polynomial functions (e.g., f(x) = x^2 + 3x - 5) and exponential functions (e.g., g(x) = 2^x) are defined for all real numbers. Therefore, their domain is:

Domain = (-∞, ∞)

4. Techniques for Finding the Range of a Function

Finding the range of a function can be more challenging than finding the domain. Here are some common techniques:

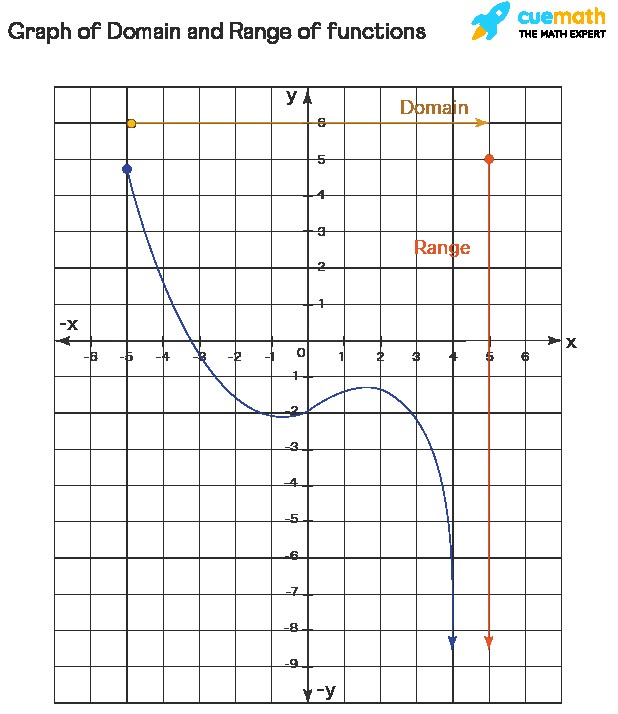
4.1. Graphing the Function

The most straightforward way to determine the range of a function is by graphing it. The range is the set of all y-values that the graph covers.

Example:

Consider the function f(x) = x^2. By graphing this function, you can see that the y-values are always greater than or equal to zero. Therefore, the range is:

Range = [0, ∞)

4.2. Analyzing the Function’s Behavior

Sometimes, you can determine the range by analyzing the function’s behavior. Consider the following:

• Minimum and Maximum Values: Does the function have a minimum or maximum value? If so, the range will be bounded by these values.
• Asymptotes: Does the function have any horizontal asymptotes? If so, the range will approach these values but may not include them.
• Increasing/Decreasing Intervals: How does the function behave as x increases or decreases? This can help you determine the possible range of y-values.

Example:

Consider the function g(x) = 1 / (x^2 + 1).

• The denominator (x^2 + 1) is always greater than or equal to 1.
• Therefore, the function g(x) is always less than or equal to 1.
• As x approaches infinity, g(x) approaches 0.

Therefore, the range is:

Range = (0, 1]

4.3. Using Inverse Functions

If you can find the inverse of a function, the domain of the inverse function is equal to the range of the original function.

Example:

Consider the function h(x) = 2x + 3.

1. Find the inverse function:
   • Replace h(x) with y: y = 2x + 3
   • Swap x and y: x = 2y + 3
   • Solve for y: y = (x - 3) / 2
   • Replace y with h^(-1)(x): h^(-1)(x) = (x - 3) / 2
2. Find the domain of the inverse function:
   • The inverse function is a linear function, so its domain is all real numbers.
3. Therefore, the range of the original function is all real numbers:

Range = (-∞, ∞)

4.4. Considering Special Functions

Certain types of functions have well-known range properties:

• Absolute Value Functions: The range of an absolute value function f(x) = |x| is always non-negative: Range = [0, ∞)
• Exponential Functions: The range of an exponential function g(x) = a^x (where a > 0) is always positive: Range = (0, ∞)
• Trigonometric Functions: The range of sine and cosine functions is [-1, 1].

5. Domain and Range of Specific Function Types

Let’s explore the domain and range of some common function types:

5.1. Linear Functions

A linear function has the form f(x) = mx + b, where ‘m’ is the slope and ‘b’ is the y-intercept.

• Domain: All real numbers: (-∞, ∞)
• Range: All real numbers: (-∞, ∞)

5.2. Quadratic Functions

A quadratic function has the form f(x) = ax^2 + bx + c, where ‘a’, ‘b’, and ‘c’ are constants. The graph of a quadratic function is a parabola.

• Domain: All real numbers: (-∞, ∞)
• Range: Depends on whether the parabola opens upwards (a > 0) or downwards (a < 0):
  • If a > 0, Range = [minimum value, ∞)
  • If a < 0, Range = (-∞, maximum value]

To find the minimum or maximum value, you can use the vertex formula: x = -b / 2a. Then, substitute this value of x back into the function to find the corresponding y-value.

5.3. Rational Functions

A rational function is a function that can be written as the ratio of two polynomials: f(x) = P(x) / Q(x).

• Domain: All real numbers except for the values that make the denominator equal to zero.
• Range: Can be more complex to determine. Look for horizontal asymptotes and analyze the function’s behavior as x approaches infinity and negative infinity.

5.4. Exponential Functions

An exponential function has the form f(x) = a^x, where ‘a’ is a constant greater than 0.

• Domain: All real numbers: (-∞, ∞)
• Range: All positive real numbers: (0, ∞)

5.5. Logarithmic Functions

A logarithmic function has the form f(x) = log_a(x), where ‘a’ is a constant greater than 0 and not equal to 1.

• Domain: All positive real numbers: (0, ∞)
• Range: All real numbers: (-∞, ∞)

5.6. Trigonometric Functions

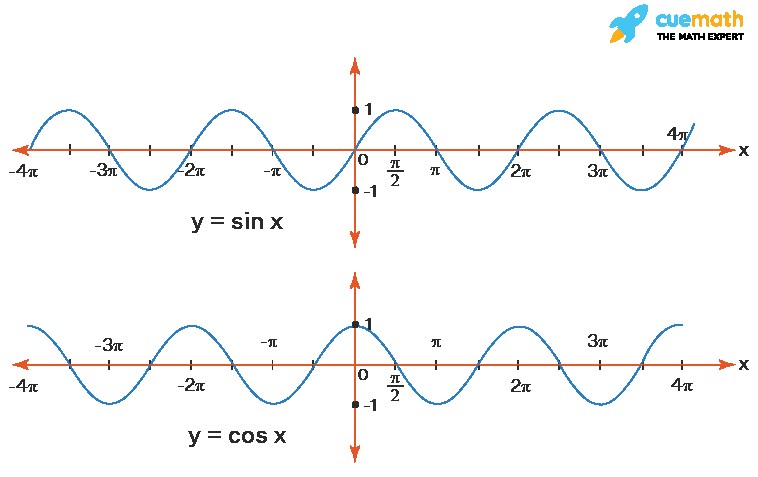
Trigonometric functions (sine, cosine, tangent, etc.) have specific domain and range properties:

Function	Domain	Range
sin(x)	All real numbers: (-∞, ∞)	[-1, 1]
cos(x)	All real numbers: (-∞, ∞)	[-1, 1]
tan(x)	All real numbers except x = (2n+1)π/2, where n is an integer	(-∞, ∞)

5.7. Absolute Value Functions

An absolute value function has the form f(x) = |x|.

• Domain: All real numbers: (-∞, ∞)
• Range: All non-negative real numbers: [0, ∞)

5.8. Square Root Functions

A square root function has the form f(x) = √x.

• Domain: All non-negative real numbers: [0, ∞)
• Range: All non-negative real numbers: [0, ∞)

6. Practical Examples and Applications

Let’s work through some practical examples to solidify your understanding:

Example 1: Modeling Projectile Motion

A projectile is launched with an initial vertical velocity of 50 m/s. The height of the projectile as a function of time is given by:

h(t) = -4.9t^2 + 50t

where h(t) is the height in meters and t is the time in seconds.

Domain:

• Time cannot be negative, so t ≥ 0.
• The projectile will eventually hit the ground, so we need to find the time when h(t) = 0:

  -4.9t^2 + 50t = 0
  t(-4.9t + 50) = 0
  t = 0 or t = 50 / 4.9 ≈ 10.2

• Therefore, the domain is [0, 10.2] seconds.

Range:

• The function is a quadratic function with a negative leading coefficient, so it has a maximum value.
• To find the maximum value, use the vertex formula: t = -b / 2a = -50 / (2 * -4.9) ≈ 5.1
• Substitute this value back into the function: h(5.1) ≈ -4.9(5.1)^2 + 50(5.1) ≈ 127.6
• Therefore, the range is [0, 127.6] meters.

Example 2: Modeling Bacterial Growth

The population of bacteria in a culture is modeled by the function:

P(t) = 1000 * e^(0.2t)

where P(t) is the population at time ‘t’ (in hours).

Domain:

• Time cannot be negative, so t ≥ 0.
• The model can theoretically continue indefinitely, so the domain is [0, ∞) hours.

Range:

• The exponential function e^(0.2t) is always positive.
• As t approaches infinity, P(t) also approaches infinity.
• At t = 0, P(0) = 1000 * e^(0) = 1000
• Therefore, the range is [1000, ∞) bacteria.

7. Advanced Techniques and Considerations

As you delve deeper into function analysis, you may encounter more complex scenarios that require advanced techniques:

• Piecewise Functions: These functions are defined by different expressions over different intervals of their domain. You need to analyze each piece separately to determine the overall domain and range.
• Implicit Functions: These functions are defined implicitly by an equation that relates x and y, rather than explicitly as y = f(x). Finding the domain and range of implicit functions can be challenging and may require implicit differentiation or other advanced techniques.
• Multivariable Functions: Functions with multiple input variables (e.g., f(x, y)) have domains and ranges that are subsets of higher-dimensional spaces. Analyzing these functions requires concepts from multivariable calculus.

8. Leveraging Expert Consultation at HOW.EDU.VN

Navigating the intricacies of domain and range can be complex, particularly with advanced functions and real-world applications. At HOW.EDU.VN, we connect you with leading experts, including PhD-level consultants, who can provide personalized guidance and solutions.

Our team of over 100 renowned PhDs offers unparalleled expertise across various mathematical domains. Whether you’re grappling with complex function analysis, seeking clarity on advanced techniques, or need assistance with real-world modeling, our experts are here to support you.

Benefits of Consulting with HOW.EDU.VN Experts:

• Personalized Guidance: Receive tailored advice and solutions specific to your unique challenges.
• Expert Insights: Gain access to the knowledge and experience of leading PhDs in mathematics.
• Time-Saving Solutions: Avoid costly errors and wasted time by leveraging our experts’ efficient problem-solving skills.
• Enhanced Understanding: Deepen your comprehension of domain and range concepts through clear explanations and practical examples.

Ready to connect with an expert?

Visit HOW.EDU.VN today and submit your questions to our team of PhDs. Let us help you unlock the full potential of functions and achieve your mathematical goals.

9. Testimonials

“I was struggling to find the domain and range of a complex piecewise function. The expert I consulted with at HOW.EDU.VN provided a clear and concise explanation that helped me understand the underlying concepts. I highly recommend their services.” – Sarah M.

“I needed help with a real-world application of function analysis. The PhD consultant at HOW.EDU.VN was able to provide a solution that was both accurate and practical. I am very grateful for their expertise.” – David L.

10. Contact Information

For expert consultation and personalized solutions, contact HOW.EDU.VN today:

• Address: 456 Expertise Plaza, Consult City, CA 90210, United States
• WhatsApp: +1 (310) 555-1212
• Website: HOW.EDU.VN

Our team of leading PhDs is ready to assist you with all your mathematical challenges.

11. FAQ About Domain and Range

Q1: What is the difference between domain and range?

A: The domain is the set of all possible input values (x-values) for which a function is defined, while the range is the set of all possible output values (y-values) that the function can produce.

Q2: How do I find the domain of a function?

A: Look for restrictions on the input values that would lead to undefined or invalid results, such as division by zero, square roots of negative numbers, or logarithms of non-positive numbers.

Q3: How do I find the range of a function?

A: Graphing the function is the most straightforward way to determine the range. You can also analyze the function’s behavior, look for minimum and maximum values, or use inverse functions.

Q4: What is the domain and range of a linear function?

A: The domain and range of a linear function are both all real numbers: (-∞, ∞).

Q5: What is the domain and range of a quadratic function?

A: The domain of a quadratic function is all real numbers: (-∞, ∞). The range depends on whether the parabola opens upwards or downwards and is bounded by the minimum or maximum value of the function.

Q6: How can HOW.EDU.VN help me with domain and range problems?

A: HOW.EDU.VN connects you with leading PhD-level experts who can provide personalized guidance, solutions, and explanations for your specific domain and range challenges.

Q7: What types of functions can HOW.EDU.VN experts help me with?

A: Our experts have expertise in a wide range of function types, including linear, quadratic, rational, exponential, logarithmic, trigonometric, absolute value, piecewise, and multivariable functions.

Q8: How do I contact HOW.EDU.VN for expert consultation?

A: You can contact HOW.EDU.VN through our website, phone, or WhatsApp. Visit HOW.EDU.VN for more information.

Q9: Is the advice I receive from HOW.EDU.VN experts confidential?

A: Yes, we prioritize the confidentiality and privacy of our clients. All consultations are conducted with the utmost discretion.

Q10: What are the benefits of consulting with a PhD expert at HOW.EDU.VN?

A: Consulting with a PhD expert at HOW.EDU.VN provides personalized guidance, expert insights, time-saving solutions, and enhanced understanding of domain and range concepts.

12. Conclusion: Empowering Your Mathematical Journey with HOW.EDU.VN

Mastering the domain and range of functions is a critical step in your mathematical journey. By understanding the concepts, applying the techniques, and leveraging the expertise available at HOW.EDU.VN, you can unlock the full potential of functions and excel in your mathematical endeavors.

Don’t hesitate to reach out to us for personalized guidance and solutions. Our team of leading PhDs is ready to support you every step of the way. Visit how.edu.vn today and submit your questions. Let us help you achieve your mathematical goals.