Finding the radius of a circle can be straightforward if you understand the fundamental formulas and relationships, and HOW.EDU.VN is here to guide you through it. This comprehensive guide will explore various methods to determine a circle’s radius, offering practical examples and expert insights for accurate calculations and problem-solving, ensuring mastery of circle geometry. Discover the secrets of circle measurements and unlock the potential of geometric precision, understanding its significance in various applications like engineering, design, and everyday problem-solving, with circle measurements and geometric calculations.
1. Understanding the Basics of Circle Geometry
Geometry is the study of shapes, sizes, relative positions of figures, and the properties of space. Circle geometry, a branch of this vast field, focuses specifically on circles, their properties, and relationships. A circle is defined as a set of points equidistant from a central point. This central point is known as the center, and the distance from the center to any point on the circle is called the radius.
1.1 Key Definitions in Circle Geometry
To effectively understand How To Find The Radius Of A Circle, it’s crucial to grasp several fundamental definitions:
- Circle: A closed, two-dimensional shape where all points are equidistant from the center.
- Center: The point inside the circle from which all points on the circle are equally distant.
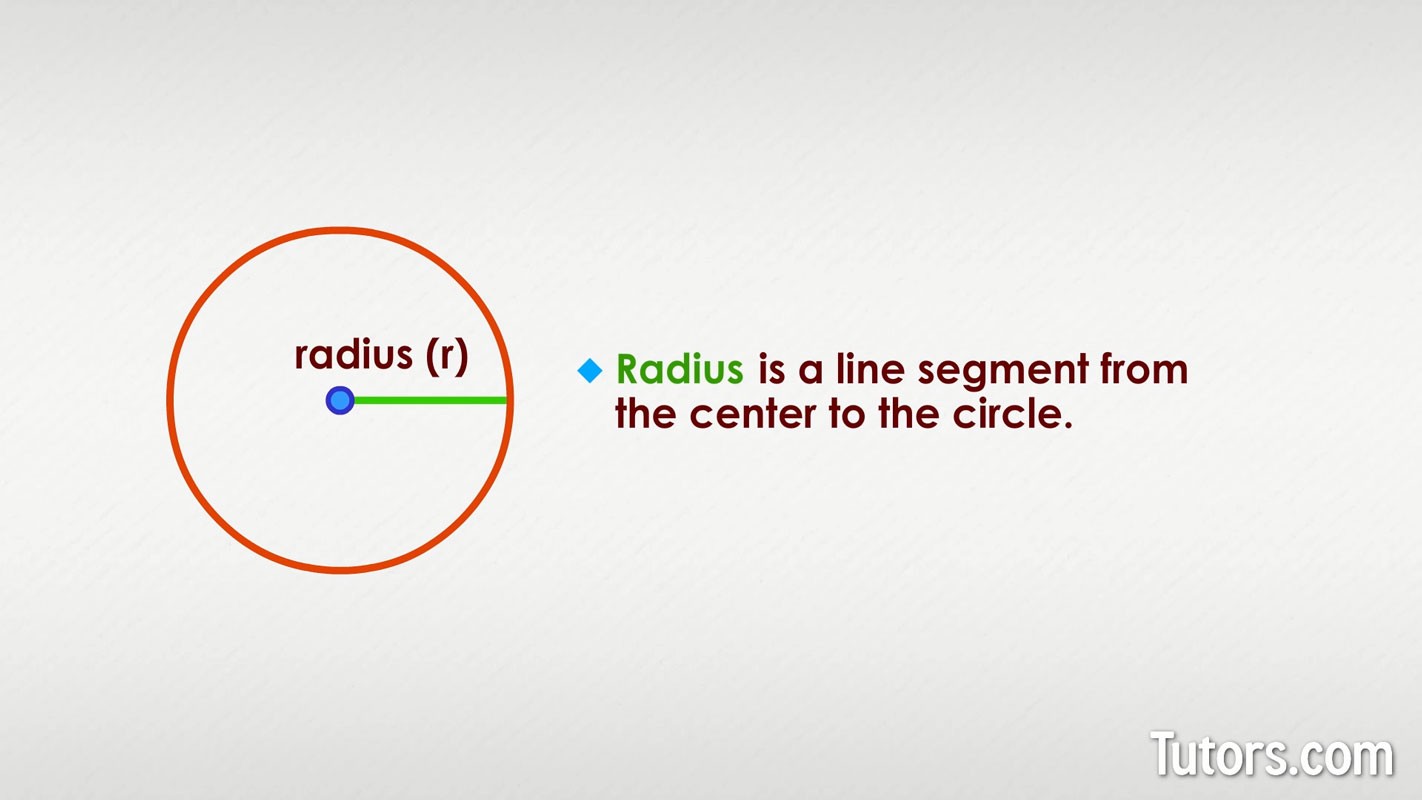
- Radius (r): The distance from the center of the circle to any point on its circumference.
- Diameter (d): A straight line passing through the center of the circle, connecting two points on the circumference. The diameter is twice the length of the radius (d = 2r).
- Circumference (C): The distance around the circle. It can be calculated using the formula C = 2πr, where π (pi) is approximately 3.14159.
- Area (A): The space enclosed within the circle. It can be calculated using the formula A = πr².
- Pi (π): A mathematical constant approximately equal to 3.14159. It represents the ratio of a circle’s circumference to its diameter.
1.2 The Significance of the Radius
The radius is not just a measurement; it is a fundamental property of a circle that dictates its size and is crucial for calculating other key parameters such as circumference and area. The radius also plays a pivotal role in various real-world applications, from engineering and architecture to design and astronomy. Understanding how to accurately determine the radius is essential for precise calculations and problem-solving in numerous fields.
2. Methods to Determine the Radius of a Circle
There are several methods to find the radius of a circle, depending on the information available. Whether you know the diameter, circumference, or area, each approach involves a specific formula to calculate the radius accurately. Below are the primary methods explained in detail.
2.1 Finding the Radius When the Diameter is Known
The diameter of a circle is a straight line that passes through the center, connecting two points on the circle’s circumference. The relationship between the radius (r) and the diameter (d) is straightforward: the radius is half the length of the diameter.
Formula:
r = d / 2
Explanation:
To find the radius, simply divide the length of the diameter by 2. This method is the most direct and easiest way to calculate the radius when the diameter is known.
Example:
If a circle has a diameter of 10 cm, the radius would be:
r = 10 cm / 2 = 5 cm
2.2 Determining the Radius When the Circumference is Known
The circumference is the distance around the circle. The relationship between the circumference (C) and the radius (r) is defined by the formula C = 2πr. To find the radius when the circumference is known, you need to rearrange this formula.
Formula:
r = C / (2π)
Explanation:
To find the radius, divide the circumference by 2π (approximately 6.28318). This method is useful when you can measure the distance around the circle but don’t have direct access to the diameter or center.
Example:
If a circle has a circumference of 25 cm, the radius would be:
r = 25 cm / (2π) ≈ 25 cm / 6.28318 ≈ 3.979 cm
2.3 Calculating the Radius When the Area is Known
The area of a circle is the space enclosed within its boundary. The relationship between the area (A) and the radius (r) is defined by the formula A = πr². To find the radius when the area is known, you need to rearrange this formula.
Formula:
r = √(A / π)
Explanation:
To find the radius, divide the area by π and then take the square root of the result. This method is particularly useful when you can calculate or measure the area of the circle, such as in design or engineering applications.
Example:
If a circle has an area of 50 cm², the radius would be:
r = √(50 cm² / π) ≈ √(50 cm² / 3.14159) ≈ √15.915 cm² ≈ 3.989 cm
2.4 Using Coordinates of Points on the Circle
In coordinate geometry, if you know the coordinates of the center and a point on the circle, you can use the distance formula to find the radius. The distance formula calculates the distance between two points in a coordinate plane.
Formula:
Given the center of the circle at point (h, k) and a point on the circle at (x, y), the radius r is:
r = √((x – h)² + (y – k)²)
Explanation:
- Identify the coordinates of the center (h, k) and a point on the circle (x, y).
- Subtract the x-coordinate of the center from the x-coordinate of the point on the circle (x – h).
- Subtract the y-coordinate of the center from the y-coordinate of the point on the circle (y – k).
- Square both results: (x – h)² and (y – k)².
- Add the squared results together.
- Take the square root of the sum to find the radius r.
Example:
If the center of the circle is at (2, 3) and a point on the circle is at (6, 6), the radius would be:
r = √((6 – 2)² + (6 – 3)²) = √(4² + 3²) = √(16 + 9) = √25 = 5
2.5 Utilizing the Circle Equation
The equation of a circle in the Cartesian plane is given by:
(x – h)² + (y – k)² = r²
where (h, k) is the center of the circle and r is the radius. If you have the equation of a circle, you can directly find the radius.
Explanation:
- Ensure the equation is in the standard form: (x – h)² + (y – k)² = r².
- Identify the value on the right side of the equation, which is r².
- Take the square root of this value to find the radius r.
Example:
If the equation of a circle is (x – 1)² + (y + 2)² = 9, then:
r² = 9
r = √9 = 3
3. Practical Examples and Applications
Understanding how to find the radius of a circle is essential in various practical scenarios. Let’s explore some real-world examples where determining the radius is crucial.
3.1 Engineering Applications
In engineering, knowing the radius of circular components is vital for design and construction. Consider designing a circular gear or a cylindrical pipe.
Example:
An engineer needs to design a circular gear that fits into a machine. The gear must have a circumference of 75 cm to mesh correctly with other components. What should the radius of the gear be?
Solution:
Using the formula r = C / (2π):
r = 75 cm / (2π) ≈ 75 cm / 6.28318 ≈ 11.937 cm
Therefore, the radius of the gear should be approximately 11.937 cm.
3.2 Architectural Design
Architects often work with circular shapes in their designs, whether it’s for domes, windows, or decorative elements.
Example:
An architect is designing a circular window for a building. The window should have an area of 3 m². What should the radius of the window be?
Solution:
Using the formula r = √(A / π):
r = √(3 m² / π) ≈ √(3 m² / 3.14159) ≈ √0.9549 m² ≈ 0.977 m
Therefore, the radius of the window should be approximately 0.977 meters.
3.3 Navigation
In navigation, particularly in maritime or aviation contexts, circles and their radii are used to define areas of operation or coverage.
Example:
A radar system has a circular coverage area. The radar can detect objects up to a distance of 50 km from its center. What is the radius of the radar’s coverage area?
Solution:
In this case, the radius is simply the maximum detection distance:
r = 50 km
Therefore, the radius of the radar’s coverage area is 50 km.
3.4 Everyday Problem Solving
Determining the radius of a circle can also be useful in everyday situations.
Example:
You have a circular rug that you want to place in a room. You know the area of the rug is 4 m². What is the radius of the rug?
Solution:
Using the formula r = √(A / π):
r = √(4 m² / π) ≈ √(4 m² / 3.14159) ≈ √1.2732 m² ≈ 1.128 m
Therefore, the radius of the rug is approximately 1.128 meters.
3.5 The Role of Pi (π)
In all the methods mentioned above, the value of Pi (π) is crucial. Pi is a mathematical constant that represents the ratio of a circle’s circumference to its diameter and is approximately equal to 3.14159. When calculating the radius using the circumference or area, using an accurate value of Pi is essential for precise results.
4. Common Mistakes to Avoid
When calculating the radius of a circle, it’s easy to make mistakes that can lead to incorrect results. Here are some common pitfalls to watch out for:
4.1 Mixing Up Diameter and Radius
One of the most common errors is confusing the diameter and radius. Remember that the diameter is twice the length of the radius (d = 2r), and the radius is half the length of the diameter (r = d / 2). Always double-check which value you are given before performing calculations.
Example:
If given a diameter of 12 cm, mistakenly using 12 cm as the radius will lead to incorrect subsequent calculations. The correct radius is 12 cm / 2 = 6 cm.
4.2 Incorrectly Applying Formulas
Using the wrong formula for the given information can lead to significant errors. Make sure to use the correct formula based on whether you know the diameter, circumference, or area.
Example:
Trying to find the radius using the circumference formula (r = C / (2π)) when you actually have the area will result in an incorrect radius. Always match the formula to the given parameter.
4.3 Math Errors
Simple arithmetic mistakes, such as miscalculating square roots or division, can lead to incorrect answers.
Example:
When finding the radius from the area, if A = 25π, calculating √25π as 5 instead of 5√π will give you the wrong radius.
4.4 Using an Inaccurate Value for Pi (π)
While approximating π as 3.14 is acceptable for quick estimations, using a more precise value (e.g., 3.14159) is crucial for accurate calculations, especially in engineering and scientific contexts.
Example:
For a circumference of 50 cm, using π = 3.14 gives r ≈ 7.96 cm, whereas using π = 3.14159 gives r ≈ 7.9577 cm. While the difference may seem small, it can be significant in precise applications.
4.5 Forgetting Units
Always include the appropriate units in your calculations and final answer. Forgetting units can lead to misunderstandings and errors, especially in practical applications.
Example:
Calculating a radius as 5 without specifying whether it is 5 cm, 5 m, or 5 inches makes the answer incomplete and potentially misleading.
4.6 Rounding Errors
Rounding too early in the calculation process can introduce inaccuracies. It is best to keep as many decimal places as possible until the final step.
Example:
If intermediate calculations yield a value of 2.3333, rounding it to 2.33 before further calculations can affect the final result, especially if multiple steps are involved.
5. Advanced Applications and Concepts
Beyond basic calculations, the radius of a circle is fundamental to various advanced mathematical and scientific concepts. Let’s explore some of these.
5.1 Calculus and Circle Geometry
In calculus, understanding the radius is crucial for solving problems related to areas, volumes, and rates of change involving circular shapes.
- Area of a Circle: The area of a circle (A = πr²) is a basic concept in integral calculus. Finding the area involves integrating over the circle’s boundary.
- Volume of a Sphere: The volume of a sphere (V = (4/3)πr³) depends directly on the radius and is calculated using integration techniques in three dimensions.
- Surface Area of a Sphere: The surface area of a sphere (SA = 4πr²) also relies on the radius and is derived using calculus.
5.2 Trigonometry and Circle Relationships
The unit circle, with a radius of 1, is a central concept in trigonometry. It is used to define trigonometric functions such as sine, cosine, and tangent.
- Unit Circle: The coordinates of points on the unit circle are given by (cos θ, sin θ), where θ is the angle formed with the positive x-axis. The radius is always 1, simplifying many trigonometric calculations.
- Trigonometric Identities: Many trigonometric identities are based on the relationships within the unit circle. Understanding the radius helps in deriving and applying these identities.
5.3 Physics and Engineering
The radius of a circle is essential in physics and engineering for analyzing rotational motion, wave phenomena, and electromagnetic fields.
- Rotational Motion: The angular velocity (ω) and tangential velocity (v) of an object moving in a circle are related by v = rω, where r is the radius. Understanding the radius is crucial for calculating these parameters.
- Wave Phenomena: In wave mechanics, circular wavefronts are common. The radius of these wavefronts describes the extent of the wave’s propagation.
- Electromagnetic Fields: The strength of electromagnetic fields around circular conductors depends on the radius of the conductor.
5.4 Complex Numbers and Circle Geometry
In complex analysis, a circle can be represented in the complex plane. The equation of a circle with center c and radius r is |z – c| = r, where z is a complex number.
- Complex Plane: Circles in the complex plane are used to visualize and analyze complex functions. The radius of these circles plays a crucial role in understanding the behavior of these functions.
- Conformal Mapping: Conformal mappings, which preserve angles locally, often involve transforming circles into other shapes. Understanding the radius helps in analyzing these transformations.
6. Leveraging Expert Guidance
Navigating complex calculations and applications involving circles can be challenging. Accessing expert guidance can significantly enhance your understanding and accuracy. At HOW.EDU.VN, we connect you with top-tier PhDs and experts who can provide personalized assistance.
6.1 Benefits of Consulting Experts at HOW.EDU.VN
- In-Depth Understanding: Experts offer deep insights into circle geometry, helping you grasp fundamental concepts and advanced applications.
- Accurate Problem Solving: Receive step-by-step guidance to solve complex problems, ensuring precision in your calculations and results.
- Customized Learning: Tailored advice to address your specific challenges, whether you’re a student, engineer, or architect.
- Real-World Applications: Understand how circle geometry applies to various fields, from engineering design to complex mathematical analysis.
6.2 How HOW.EDU.VN Can Help
HOW.EDU.VN offers a unique platform to connect with seasoned professionals who can provide expert consultations. Whether you need help with a specific problem, want to deepen your understanding, or require assistance with a project, our experts are here to support you.
- Personalized Consultations: Engage in one-on-one sessions with experts who can answer your questions and provide tailored solutions.
- Detailed Explanations: Receive clear, concise explanations of complex concepts, making it easier to apply them in your work.
- Practical Examples: Explore real-world examples and case studies that illustrate the practical applications of circle geometry.
- Project Assistance: Get support for your projects, ensuring accuracy and efficiency in your calculations and designs.
6.3 Connect With Our Experts
Don’t let challenging problems hold you back. Connect with our team of experienced PhDs and experts at HOW.EDU.VN for personalized guidance and support. Enhance your understanding of circle geometry and achieve your goals with confidence.
7. Practical Exercises
To reinforce your understanding of how to find the radius of a circle, let’s go through some practical exercises. These exercises cover different scenarios and require you to apply the formulas and concepts discussed earlier.
7.1 Exercise 1: Finding the Radius from the Diameter
Problem: A circular table has a diameter of 1.8 meters. What is the radius of the table?
Solution:
- Formula: r = d / 2
- Given: Diameter (d) = 1.8 meters
- Calculation: r = 1.8 m / 2 = 0.9 meters
- Answer: The radius of the circular table is 0.9 meters.
7.2 Exercise 2: Calculating the Radius from the Circumference
Problem: A circular garden has a circumference of 35 meters. Find the radius of the garden.
Solution:
- Formula: r = C / (2π)
- Given: Circumference (C) = 35 meters
- Calculation: r = 35 m / (2π) ≈ 35 m / 6.28318 ≈ 5.570 meters
- Answer: The radius of the circular garden is approximately 5.570 meters.
7.3 Exercise 3: Determining the Radius from the Area
Problem: A circular pond has an area of 75 square meters. What is the radius of the pond?
Solution:
- Formula: r = √(A / π)
- Given: Area (A) = 75 square meters
- Calculation: r = √(75 m² / π) ≈ √(75 m² / 3.14159) ≈ √23.873 m² ≈ 4.886 meters
- Answer: The radius of the circular pond is approximately 4.886 meters.
7.4 Exercise 4: Using Coordinates to Find the Radius
Problem: The center of a circle is at point (1, -2), and a point on the circle is at (4, 2). Find the radius of the circle.
Solution:
- Formula: r = √((x – h)² + (y – k)²)
- Given: Center (h, k) = (1, -2), Point on circle (x, y) = (4, 2)
- Calculation: r = √((4 – 1)² + (2 – (-2))²) = √(3² + 4²) = √(9 + 16) = √25 = 5
- Answer: The radius of the circle is 5 units.
7.5 Exercise 5: Applying the Circle Equation
Problem: The equation of a circle is (x + 3)² + (y – 1)² = 16. Find the radius of the circle.
Solution:
- Equation form: (x – h)² + (y – k)² = r²
- Given: (x + 3)² + (y – 1)² = 16
- Identify r²: r² = 16
- Calculation: r = √16 = 4
- Answer: The radius of the circle is 4 units.
8. How To Ask Questions To Our PHD
At HOW.EDU.VN, we understand the importance of getting accurate and reliable answers to your questions, especially when dealing with complex topics like finding the radius of a circle. Our platform offers a unique opportunity to connect with experienced PhDs and experts who can provide detailed, personalized responses. Here’s how you can effectively ask questions to our experts:
8.1 Prepare Your Questions
Before you submit your question, take some time to prepare it thoroughly. This will help our experts understand your needs and provide the most relevant and helpful answers.
- Be Specific: Clearly state what you are trying to find out. For example, instead of asking “How do I find the radius?”, ask “How do I find the radius of a circle when I only know the area?”
- Provide Context: Include any relevant background information. Are you working on a specific problem? What have you tried so far? The more context you provide, the better our experts can assist you.
- Break Down Complex Questions: If your question involves multiple steps or concepts, break it down into smaller, more manageable parts. This makes it easier for the expert to address each aspect individually.
8.2 Utilize Clear and Concise Language
When writing your question, use language that is easy to understand. Avoid jargon or overly technical terms unless you are certain that the expert is familiar with them.
- Use Proper Grammar and Spelling: This ensures that your question is clear and professional.
- Be Concise: Get straight to the point. Avoid unnecessary details or rambling.
8.3 Provide Relevant Data
If your question involves a specific calculation or problem, provide all the necessary data. This might include measurements, equations, or other relevant information.
- Include Units: Always specify the units of measurement (e.g., meters, centimeters, square feet).
- Double-Check Your Data: Make sure that all the information you provide is accurate.
8.4 Example of a Good Question
Here’s an example of a well-prepared question:
“I am trying to find the radius of a circular swimming pool. I know the area of the pool is 150 square meters. I have tried using the formula r = √(A / π), but I am not sure if I am applying it correctly. Could you please walk me through the steps to calculate the radius in this case, ensuring I use the correct units?”
8.5 Submitting Your Question on HOW.EDU.VN
Once you have prepared your question, follow these steps to submit it on HOW.EDU.VN:
- Create an Account: If you don’t already have one, create an account on HOW.EDU.VN.
- Navigate to the Ask an Expert Section: Find the section on our website where you can submit questions to experts.
- Fill Out the Question Form: Enter your question in the provided form, including all relevant details and data.
- Review Your Question: Before submitting, double-check your question to ensure it is clear, concise, and includes all necessary information.
- Submit Your Question: Click the submit button to send your question to our experts.
8.6 What to Expect After Submitting Your Question
After you submit your question, one of our experienced PhDs or experts will review it and provide a detailed response.
- Timely Responses: We strive to provide responses as quickly as possible, typically within 24-48 hours.
- Detailed Answers: Our experts will provide thorough explanations, step-by-step guidance, and practical examples to help you understand the answer.
- Follow-Up Questions: If you need further clarification, you can ask follow-up questions to ensure you fully understand the topic.
8.7 Benefits of Asking Questions on HOW.EDU.VN
- Expert Knowledge: Get answers from experienced PhDs and professionals with deep knowledge in their fields.
- Personalized Assistance: Receive tailored advice and solutions that address your specific needs.
- Reliable Information: Ensure that you are getting accurate and trustworthy information.
- Enhanced Learning: Deepen your understanding of complex topics through detailed explanations and practical examples.
9. Real-World Examples of Expert Consultations
To illustrate the value of consulting with experts, here are some real-world examples of how expert consultations at HOW.EDU.VN have helped individuals and professionals solve problems related to circle geometry.
9.1 Engineering Design
Scenario: An engineer was designing a new circular water tank and needed to calculate the precise radius to ensure it could hold a specific volume of water.
Challenge: The engineer was unsure about the correct formula to use, given the constraints of the tank’s height and desired volume.
Solution: Through a consultation with a structural engineering expert at HOW.EDU.VN, the engineer received detailed guidance on the appropriate formulas and calculations. The expert provided a step-by-step explanation, ensuring the engineer understood how to account for all variables.
Outcome: The engineer accurately calculated the radius, leading to a successful tank design that met all specifications.
9.2 Architectural Planning
Scenario: An architect was designing a circular courtyard for a new building and needed to determine the radius that would maximize the use of space while maintaining aesthetic appeal.
Challenge: The architect was struggling to balance the courtyard’s size with the building’s overall design and was unsure how to optimize the space effectively.
Solution: The architect consulted with a design expert at HOW.EDU.VN, who provided insights into spatial planning and aesthetic considerations. The expert helped the architect understand how different radii would impact the overall design and suggested ways to incorporate the courtyard seamlessly.
Outcome: The architect finalized a design that optimized space utilization and enhanced the building’s aesthetic appeal, resulting in a visually stunning and functional courtyard.
9.3 Navigation System Development
Scenario: A software developer was creating a navigation system that relied on circular geofences to alert users when they entered specific areas.
Challenge: The developer needed to accurately calculate the radius of each geofence to ensure the system worked reliably.
Solution: The developer consulted with a GPS and navigation expert at HOW.EDU.VN, who provided detailed explanations of the formulas and algorithms needed to calculate the radius accurately. The expert also helped the developer troubleshoot issues related to coordinate systems and map projections.
Outcome: The navigation system functioned flawlessly, providing accurate alerts and enhancing user experience.
9.4 Educational Support
Scenario: A student was struggling with a calculus assignment that involved finding the area of a circle using integration.
Challenge: The student was having difficulty understanding the integration process and how it related to the circle’s radius.
Solution: The student connected with a mathematics tutor at HOW.EDU.VN, who provided a step-by-step explanation of the integration process. The tutor helped the student visualize the problem and understand how the radius played a key role in the calculation.
Outcome: The student successfully completed the assignment and gained a deeper understanding of calculus concepts related to circle geometry.
9.5 DIY Home Improvement
Scenario: A homeowner was planning to install a circular patio in their backyard and needed to calculate the radius to ensure it fit perfectly within the available space.
Challenge: The homeowner was unsure how to measure the area accurately and determine the appropriate radius.
Solution: The homeowner consulted with a home improvement expert at HOW.EDU.VN, who provided guidance on measuring techniques and radius calculation. The expert also offered tips on laying out the patio to ensure it was perfectly circular.
Outcome: The homeowner successfully installed the patio, enhancing the beauty and functionality of their backyard.
10. Why Choose HOW.EDU.VN
Choosing the right platform for expert consultations is crucial for receiving accurate, reliable, and personalized assistance. HOW.EDU.VN stands out as a premier choice for connecting with top-tier PhDs and experts. Here are several reasons why you should choose HOW.EDU.VN:
10.1 Access to Top-Tier Experts
HOW.EDU.VN provides access to a network of highly qualified PhDs and experts who possess extensive knowledge and experience in their respective fields. Our experts are carefully selected for their expertise, communication skills, and commitment to providing exceptional guidance.
- Vetted Professionals: All our experts undergo a rigorous vetting process to ensure they meet our high standards for knowledge and professionalism.
- Diverse Expertise: Our network includes experts from a wide range of fields, including engineering, mathematics, architecture, and more, ensuring you can find the right expert for your specific needs.
- Proven Track Record: Our experts have a proven track record of providing accurate and insightful consultations, helping individuals and professionals achieve their goals.
10.2 Personalized Consultations
We understand that every individual has unique needs and challenges. That’s why we offer personalized consultations tailored to your specific requirements.
- One-on-One Sessions: Engage in one-on-one sessions with experts who can answer your questions, provide detailed explanations, and offer customized solutions.
- Tailored Advice: Receive advice and guidance that is specifically tailored to your situation, whether you’re a student, engineer, architect, or DIY enthusiast.
- Flexible Scheduling: Schedule consultations at a time that is convenient for you, ensuring you can get the help you need when you need it.
10.3 Reliable and Accurate Information
At HOW.EDU.VN, we are committed to providing reliable and accurate information. You can trust that the advice and guidance you receive from our experts is based on sound principles and best practices.
- Fact-Checked Content: All our content is fact-checked to ensure accuracy and reliability.
- Up-to-Date Information: Our experts stay up-to-date with the latest developments in their fields, ensuring you receive the most current information.
- Evidence-Based Guidance: Our experts provide guidance that is based on evidence and proven methodologies, ensuring you can make informed decisions.
10.4 User-Friendly Platform
Our platform is designed to be user-friendly and easy to navigate. You can quickly find the experts you need, submit your questions, and schedule consultations with ease.
- Intuitive Interface: Our website is designed with an intuitive interface that makes it easy to find the information and resources you need.
- Seamless Communication: Communicate with experts seamlessly through our platform, ensuring you can get your questions answered and receive the guidance you need.
- Mobile Accessibility: Access our platform from any device, allowing you to get help on the go.
10.5 Comprehensive Support
We offer comprehensive support to ensure you have a positive experience on our platform.
- Customer Support: Our customer support team is available to answer your questions and provide assistance with any issues you may encounter.
- Resource Library: Access a library of resources, including articles, tutorials, and FAQs, to enhance your understanding of various topics.
- Community Forum: Connect with other users in our community forum to share ideas, ask questions, and learn from each other.
10.6 Success Stories
Our platform has helped countless individuals and professionals achieve their goals.
- Improved Grades: Students have improved their grades by receiving personalized tutoring and homework help from our experts.
- Successful Projects: Professionals have successfully completed projects by receiving expert guidance on design, calculations, and problem-solving.
- Enhanced Knowledge: Individuals have enhanced their knowledge and skills by participating in our online courses and workshops.
Ready to unlock your full potential? Connect with our team of experienced PhDs and experts at HOW.EDU.VN for personalized guidance and support. Whether you’re a student, engineer, architect, or DIY enthusiast, we are here to help you achieve your goals with confidence.
Address: 456 Expertise Plaza, Consult City, CA 90210, United States
Whatsapp: +1 (310) 555-1212
Website: HOW.EDU.VN
Seeking expert advice is a sign of strength, and at HOW.EDU.VN, we’re committed to empowering you with the knowledge and support you need to succeed. Contact us today and let us help you achieve your full potential.
FAQ: Finding the Radius of a Circle
-
What is the radius of a circle?
The radius of a circle is the distance from the center of the circle to any point on its circumference.
-
How do I find the radius if I know the diameter?
Divide the diameter by 2: r = d / 2.
-
What is the formula to find the radius if I know the circumference?
The formula is: r = C / (2π).
-
How can I calculate the radius if I know the area of the circle?
Use the formula: r = √(A / π).
-
Why is knowing the radius important?
The radius is fundamental for calculating other properties of the circle, such as area and circumference, and is crucial in various applications like engineering and design.
-
What is the value of π (pi) and why is it important in radius calculations?
π (pi) is a mathematical constant approximately equal to 3.14159. It represents the ratio of a circle’s circumference to its diameter and is essential for accurate radius calculations.
-
What are some common mistakes to avoid when calculating the radius?
Common mistakes include confusing the diameter and radius, using incorrect formulas, making math errors, and using an inaccurate value for π.
-
How can HOW.EDU.VN help me with understanding circle geometry?
HOW.EDU.VN connects you with top-tier PhDs and experts who can provide personalized assistance, detailed explanations, and practical examples to enhance your understanding of circle geometry.
-
Can I get help with specific problems or projects related to circle geometry on HOW.EDU.VN?
Yes, HOW.EDU.VN offers personalized consultations where experts can provide tailored advice, detailed explanations, and practical examples to help you with specific problems or projects.
-
How do I ask a question to the experts on how.edu.vn?
Create an account, navigate to the “Ask an Expert” section, fill out the question form with specific details and relevant data, and submit your question for a detailed response from our experts.