Understanding the volume of a cylinder is a fundamental concept in geometry and has practical applications in everyday life, from calculating the capacity of storage tanks to understanding the amount of liquid in a can. This guide will provide a detailed explanation of how to calculate the volume of a cylinder, including the formula, step-by-step instructions, examples, and answers to frequently asked questions.
Understanding the Basics of a Cylinder
Before diving into the calculation, let’s define what a cylinder is. In geometry, a cylinder is a three-dimensional solid shape that has two parallel circular bases connected by a curved surface. Think of common objects like cans of soup, pipes, or even some drinking glasses – these are all cylinders or cylindrical in shape.
To calculate the volume of a cylinder, you need to understand two key measurements:
- Radius (r): The radius is the distance from the center of the circular base to any point on its circumference. It’s half the diameter.
- Height (h): The height is the perpendicular distance between the two circular bases.
The Formula for the Volume of a Cylinder
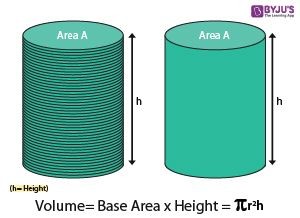
The volume of a cylinder is calculated by finding the area of its circular base and then multiplying it by the height. The formula is derived from the basic principle that volume is the area of the base times the height, applicable to prisms and cylinders alike.
Since the base of a cylinder is a circle, its area is given by the formula for the area of a circle: πr².
Therefore, the formula for the volume (V) of a cylinder is:
V = πr²h
Where:
- V is the volume of the cylinder
- π (pi) is a mathematical constant, approximately equal to 3.14159. For practical purposes, 3.14 or 22/7 are often used.
- r is the radius of the circular base
- h is the height of the cylinder
The volume is expressed in cubic units (e.g., cubic centimeters, cubic meters, cubic inches, cubic feet), reflecting that it is a three-dimensional measurement.
Step-by-Step Guide to Calculate Cylinder Volume
Let’s break down How To Find The Volume Of A Cylinder into easy-to-follow steps:
- Identify the Radius (r) of the Base: The radius is crucial. If you are given the diameter, remember to divide it by 2 to get the radius.
- Determine the Height (h) of the Cylinder: The height is the perpendicular distance between the bases. Ensure both radius and height are in the same units of measurement.
- Square the Radius (r²): Multiply the radius by itself.
- Multiply by Pi (π): Multiply the result from step 3 by pi (approximately 3.14 or 22/7). This gives you the area of the circular base.
- Multiply by the Height (h): Multiply the area of the base (from step 4) by the height of the cylinder. This final result is the volume of the cylinder.
- State the Volume in Cubic Units: Remember to express your answer in cubic units corresponding to the units used for radius and height (e.g., cm³, m³, in³).
Example Calculations
Let’s work through a couple of examples to solidify your understanding.
Example 1: Finding the Volume Given Radius and Height
Suppose you have a cylinder with a radius of 5 cm and a height of 10 cm. Let’s calculate its volume.
- Radius (r) = 5 cm
- Height (h) = 10 cm
- *r² = 5 cm 5 cm = 25 cm²**
- *πr² = 3.14 25 cm² = 78.5 cm²** (Area of the base)
- *V = πr²h = 78.5 cm² 10 cm = 785 cm³**
Therefore, the volume of the cylinder is 785 cubic centimeters.
Example 2: Finding the Volume Given Diameter and Height
Imagine a cylindrical water tank with a diameter of 2 meters and a height of 3 meters. First, we need to find the radius.
- Diameter = 2 meters, so Radius (r) = Diameter / 2 = 2 meters / 2 = 1 meter
- Height (h) = 3 meters
- *r² = 1 meter 1 meter = 1 m²**
- *πr² = 3.14 1 m² = 3.14 m²** (Area of the base)
- *V = πr²h = 3.14 m² 3 meters = 9.42 m³**
The volume of the water tank is 9.42 cubic meters.
Volume of a Hollow Cylinder
A hollow cylinder is like a pipe, having both an outer and inner radius. To find the volume of a hollow cylinder, you need to calculate the volume of the outer cylinder and subtract the volume of the inner cylindrical space.
Let:
- R be the outer radius
- r be the inner radius
- h be the height of the hollow cylinder
The formula for the volume (V) of a hollow cylinder is:
V = πh(R² – r²)
This formula essentially calculates the area of the annular region (the ring between the two circles) and multiplies it by the height.
Volume of a Cylinder in Liters and Other Units
Sometimes, you might need to convert the volume of a cylinder from cubic units to liters, gallons, or other units of capacity, especially when dealing with liquids.
Conversion Factors to Remember:
- 1 liter = 1000 cubic centimeters (cm³)
- 1 cubic meter (m³) = 1000 liters
- 1 US gallon ≈ 3785.41 cubic centimeters (cm³)
For instance, if you calculated the volume of a container to be 5000 cm³, its volume in liters would be 5000 cm³ / 1000 cm³/liter = 5 liters.
Surface Area vs. Volume of a Cylinder (Briefly)
While this article focuses on volume, it’s useful to briefly differentiate it from surface area. The surface area of a cylinder is the total area covering its outer surface, including the top and bottom bases and the curved side. The formula for the total surface area (A) of a cylinder is:
A = 2πr² + 2πrh
Where:
- 2πr² represents the area of the two circular bases
- 2πrh represents the lateral surface area (the curved side)
Volume, on the other hand, measures the space inside the cylinder. Understanding both volume and surface area is important in various applications, but they represent different properties of the cylinder.
Frequently Asked Questions (FAQs)
Q1: What is the volume of a cylinder?
The volume of a cylinder is the amount of space it occupies, or its capacity to hold a substance. It’s measured in cubic units and calculated using the formula V = πr²h.
Q2: How do you find the volume of a cylinder if you know the diameter instead of the radius?
If you know the diameter (d), remember that the radius (r) is half the diameter (r = d/2). Substitute d/2 for r in the volume formula: V = π(d/2)²h = (πd²h)/4.
Q3: What are the units for the volume of a cylinder?
Volume is measured in cubic units. Common units include cubic centimeters (cm³), cubic meters (m³), cubic inches (in³), and cubic feet (ft³). When dealing with liquids, volume is often expressed in liters or gallons.
Q4: How does doubling the radius affect the volume of a cylinder?
If you double the radius of a cylinder while keeping the height constant, the volume becomes four times larger. This is because the radius is squared in the volume formula (V = πr²h). If r becomes 2r, then V becomes π(2r)²h = 4πr²h.
Q5: What happens to the volume if you halve the height of a cylinder?
If you halve the height of a cylinder while keeping the radius constant, the volume is also halved. Since volume is directly proportional to height (V = πr²h), if h becomes h/2, then V becomes πr²(h/2) = (1/2)πr²h.
Q6: Can you calculate the volume of a cylinder in liters directly?
No, the formula V = πr²h gives the volume in cubic units. To get the volume in liters, you first calculate the volume in cubic centimeters (cm³) and then convert to liters using the conversion factor 1 liter = 1000 cm³.
Q7: What is the difference between volume and capacity of a cylinder?
In practical terms, volume and capacity are often used interchangeably, especially when discussing containers. Volume refers to the space occupied by the cylinder itself, while capacity refers to the amount a container can hold, which is numerically equal to its internal volume.
Conclusion
Calculating the volume of a cylinder is a straightforward process once you understand the formula and the components involved. By following the steps outlined in this guide and practicing with examples, you can confidently find the volume of any cylinder, whether it’s for a school problem or a real-world application. Remember to always use consistent units and pay attention to whether you are given the radius or diameter. Understanding cylinder volume is a valuable skill in mathematics and beyond.