How to Find Velocity: A Comprehensive Guide

In the realm of physics, understanding motion is fundamental, and velocity plays a crucial role in describing this phenomenon. When you’re calculating velocity, you’re determining how fast an object moves from its original position, with respect to a frame of reference, and a function of time. That means an object’s velocity will be equal to the object’s speed and direction of motion. At HOW.EDU.VN, we connect you with leading physics experts who can provide personalized guidance on velocity calculations and related concepts. Learn the nuances of velocity, displacement, and time, ensuring accurate and insightful analyses of motion with our experts.

1. Understanding the Basics of Velocity

Velocity is a fundamental concept in physics that describes the rate at which an object changes its position. Unlike speed, which only measures how fast an object is moving, velocity also includes the direction of motion. This makes velocity a vector quantity, meaning it has both magnitude (speed) and direction.

1.1. Defining Velocity

Velocity is defined as the rate of change of displacement. Displacement is the shortest distance between an object’s initial and final positions, along with the direction of travel. Therefore, velocity tells us how quickly an object is moving and in what direction.

For instance, consider a car traveling at 60 miles per hour. This is its speed. However, if we say the car is traveling at 60 miles per hour due north, we are describing its velocity. The direction “north” adds the necessary vector component to the speed.

1.2. Key Differences Between Speed and Velocity

It’s crucial to differentiate between speed and velocity. Speed is a scalar quantity, meaning it only has magnitude. Velocity, on the other hand, is a vector quantity, possessing both magnitude and direction.

Feature	Speed	Velocity
Definition	Rate of distance covered	Rate of displacement
Type	Scalar	Vector
Magnitude	Yes	Yes
Direction	No	Yes
Formula	Speed = Distance / Time	Velocity = Displacement / Time
Example	60 mph	60 mph due north

Understanding this distinction is essential for accurate calculations and interpretations in physics problems. If you need further clarification, our expert physicists at HOW.EDU.VN are available to provide detailed explanations and examples.

1.3. Importance of Direction in Velocity

The direction component of velocity is what distinguishes it from speed. This direction can be expressed in various ways, such as:

• Cardinal Directions: North, South, East, West
• Angles: Degrees relative to a reference point (e.g., 30 degrees from the horizontal)
• Vectors: Using components in a coordinate system (e.g., i, j, k)

The direction is crucial because it affects how we analyze motion. For example, two objects moving at the same speed but in opposite directions have different velocities. This becomes particularly important in scenarios involving collisions, relative motion, and navigation.

2. The Velocity Formula: A Detailed Breakdown

The velocity formula is a cornerstone of physics, allowing us to quantify and analyze motion. It provides a straightforward method for calculating velocity when displacement and time are known.

2.1. Basic Formula: Velocity = Displacement / Time

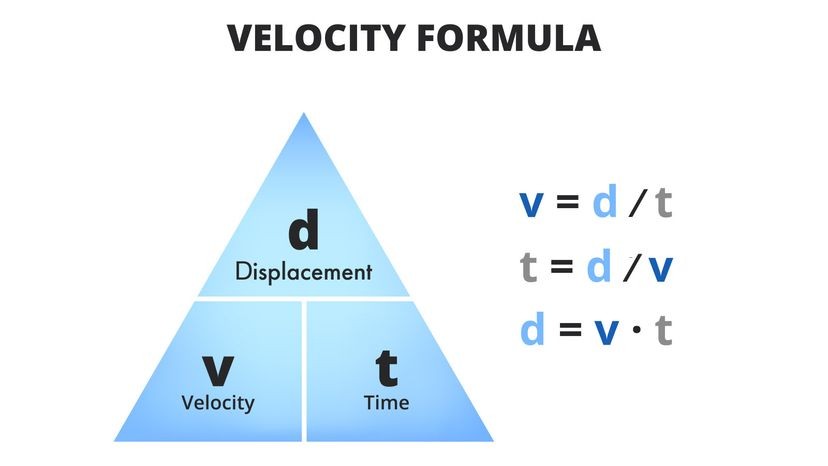
The fundamental formula for velocity is expressed as:

v = d / t

Where:

• v represents velocity
• d represents displacement
• t represents time

This formula states that velocity is equal to the displacement divided by the time taken for that displacement to occur. The units for velocity are typically meters per second (m/s) or miles per hour (mph), depending on the units used for displacement and time.

2.2. Understanding Displacement (d)

Displacement is the change in position of an object. It is a vector quantity, meaning it has both magnitude and direction. To calculate displacement, you need to know the object’s initial and final positions.

d = final position - initial position

For example, if an object starts at position x₁ = 2 meters and ends at position x₂ = 8 meters, the displacement is:

d = 8 m - 2 m = 6 m

The object has moved 6 meters in the positive direction. If the object moves back to x₁ = 2 meters, the total displacement would be:

d = 2 m - 8 m = -6 m

This indicates a displacement of 6 meters in the negative direction.

2.3. Measuring Time (t)

Time is a scalar quantity that measures the duration of an event. In the velocity formula, time represents the interval during which the displacement occurs. The standard unit for time is seconds (s), but it can also be measured in minutes, hours, or other appropriate units.

When using the velocity formula, ensure that the time unit is consistent with the displacement unit. For example, if displacement is measured in meters, time should be measured in seconds to obtain velocity in meters per second.

2.4. Practical Examples of Using the Formula

Let’s consider a few practical examples to illustrate how to use the velocity formula:

Example 1: A cyclist travels 100 meters north in 20 seconds. What is the cyclist’s velocity?

v = d / t
v = 100 m / 20 s
v = 5 m/s north

The cyclist’s velocity is 5 meters per second north.

Example 2: A train travels 500 kilometers east in 5 hours. What is the train’s velocity?

v = d / t
v = 500 km / 5 h
v = 100 km/h east

The train’s velocity is 100 kilometers per hour east.

Example 3: A bird flies from its nest to a tree 25 meters away and returns to the nest. The entire trip takes 10 seconds. What is the bird’s average velocity?

Since the bird returns to its starting point, the displacement is 0 meters.

v = d / t
v = 0 m / 10 s
v = 0 m/s

The bird’s average velocity is 0 meters per second.

These examples highlight the importance of considering both distance and direction when calculating velocity. For personalized assistance with your specific physics problems, connect with our expert tutors at HOW.EDU.VN.

3. Advanced Concepts in Velocity Calculations

While the basic velocity formula is straightforward, there are several advanced concepts that provide a more nuanced understanding of motion. These include average velocity, instantaneous velocity, and relative velocity.

3.1. Average Velocity

Average velocity is the total displacement divided by the total time taken. It represents the overall velocity of an object over a given period, regardless of any variations in speed or direction during that period.

Average velocity = Total displacement / Total time

For example, if a car travels 200 kilometers east in 4 hours and then 100 kilometers west in 2 hours, the average velocity is calculated as follows:

Total displacement = 200 km (east) - 100 km (west) = 100 km (east)
Total time = 4 hours + 2 hours = 6 hours
Average velocity = 100 km / 6 h = 16.67 km/h east

The average velocity of the car is 16.67 kilometers per hour east.

3.2. Instantaneous Velocity

Instantaneous velocity is the velocity of an object at a specific moment in time. It is the limit of the average velocity as the time interval approaches zero. In calculus terms, instantaneous velocity is the derivative of the position function with respect to time.

v(t) = lim Δt→0 Δd / Δt = dd/dt

Where:

• v(t) is the instantaneous velocity at time t
• Δd is the change in displacement
• Δt is the change in time
• dd/dt is the derivative of displacement with respect to time

Instantaneous velocity is crucial for understanding the motion of objects that are constantly changing speed or direction. For instance, the speedometer in a car displays the instantaneous speed, which is the magnitude of the instantaneous velocity.

3.3. Relative Velocity

Relative velocity is the velocity of an object with respect to another object or frame of reference. It is particularly important in scenarios where multiple objects are in motion.

To calculate relative velocity, you subtract the velocity of the reference frame from the velocity of the object.

v(A relative to B) = v(A) - v(B)

Where:

• v(A relative to B) is the velocity of object A relative to object B
• v(A) is the velocity of object A
• v(B) is the velocity of object B

For example, if two cars are moving in the same direction, car A at 60 mph and car B at 40 mph, the relative velocity of car A with respect to car B is:

v(A relative to B) = 60 mph - 40 mph = 20 mph

Car A is moving 20 mph faster than car B.

If the cars are moving in opposite directions, car A at 60 mph east and car B at 40 mph west, the relative velocity of car A with respect to car B is:

v(A relative to B) = 60 mph (east) - (-40 mph) (west) = 100 mph (east)

Car A is moving 100 mph faster than car B, relative to car B.

4. Factors Affecting Velocity

Several factors can influence an object’s velocity, including external forces, air resistance, and the medium through which the object is moving. Understanding these factors is crucial for accurate velocity calculations and predictions.

4.1. Impact of External Forces

External forces, such as gravity, friction, and applied forces, can significantly affect an object’s velocity. According to Newton’s Second Law of Motion, the net force acting on an object is equal to the mass of the object multiplied by its acceleration.

F = ma

Where:

• F is the net force
• m is the mass
• a is the acceleration

Acceleration is the rate of change of velocity. Therefore, a net force will cause an object to accelerate, changing its velocity. For example, gravity causes objects to accelerate downwards, increasing their velocity until they reach terminal velocity due to air resistance.

4.2. Air Resistance and Its Effects

Air resistance, also known as drag, is a force that opposes the motion of an object through the air. The magnitude of air resistance depends on several factors, including the object’s shape, size, and velocity, as well as the density of the air.

Air resistance can significantly reduce an object’s velocity, especially at high speeds. For example, a skydiver experiences increasing air resistance as they fall, eventually reaching a terminal velocity where the force of air resistance equals the force of gravity.

4.3. Influence of Medium on Velocity

The medium through which an object moves can also affect its velocity. For example, an object moving through water experiences more resistance than an object moving through air. This is because water is denser and more viscous than air.

The density and viscosity of the medium affect the drag force, which in turn affects the object’s velocity. In general, the denser and more viscous the medium, the lower the object’s velocity.

5. Practical Applications of Velocity

Velocity is not just a theoretical concept; it has numerous practical applications in various fields, including engineering, sports, and navigation.

5.1. Velocity in Engineering

In engineering, velocity is used to design and analyze systems involving motion, such as vehicles, machines, and structures. For example, civil engineers use velocity to calculate the flow rate of water in pipes and channels, while mechanical engineers use velocity to design engines and turbines.

Aerospace engineers rely heavily on velocity calculations to design aircraft and spacecraft. They need to understand how air resistance and thrust affect the velocity of these vehicles to ensure safe and efficient flight.

5.2. Velocity in Sports

Velocity is a crucial factor in many sports. Athletes strive to maximize their velocity to achieve better performance. For example, sprinters aim to achieve high velocities to win races, while baseball pitchers try to throw the ball at high velocities to strike out batters.

Coaches and trainers use velocity measurements to assess athletes’ performance and identify areas for improvement. They may use devices such as radar guns and accelerometers to measure velocity and track progress over time.

5.3. Velocity in Navigation

In navigation, velocity is used to determine the position and direction of a vehicle or vessel. Pilots and sailors use velocity measurements to calculate their speed and heading, which are essential for reaching their destination safely and efficiently.

Modern navigation systems, such as GPS, use satellite signals to determine velocity with high accuracy. These systems can provide real-time velocity information, allowing for precise navigation in various environments.

6. Common Mistakes to Avoid When Calculating Velocity

Calculating velocity can be challenging, and it’s easy to make mistakes if you’re not careful. Here are some common mistakes to avoid:

6.1. Confusing Speed and Velocity

One of the most common mistakes is confusing speed and velocity. Remember that speed is a scalar quantity, while velocity is a vector quantity. Always include the direction when calculating and expressing velocity.

6.2. Incorrectly Calculating Displacement

Displacement is the change in position, not the total distance traveled. Make sure to calculate displacement correctly by subtracting the initial position from the final position.

6.3. Using Inconsistent Units

When using the velocity formula, ensure that all units are consistent. For example, if displacement is measured in meters, time should be measured in seconds to obtain velocity in meters per second.

6.4. Neglecting Air Resistance and Other Forces

In real-world scenarios, air resistance and other forces can significantly affect velocity. Neglecting these forces can lead to inaccurate calculations and predictions.

7. How HOW.EDU.VN Can Help You Master Velocity

At HOW.EDU.VN, we understand the challenges of mastering physics concepts like velocity. That’s why we offer personalized tutoring and expert guidance to help you succeed.

7.1. Access to Expert Tutors

We connect you with experienced physics tutors who can provide one-on-one instruction and answer your questions. Our tutors have advanced degrees in physics and a passion for teaching. They can help you understand the concepts, work through problems, and build confidence in your abilities.

7.2. Personalized Learning Plans

We create personalized learning plans tailored to your specific needs and goals. Whether you’re struggling with basic concepts or need help with advanced topics, our tutors can design a plan that works for you.

7.3. Step-by-Step Problem Solving

Our tutors guide you through step-by-step problem solving, helping you develop critical thinking skills and a deeper understanding of the material. They can show you how to apply the velocity formula and other physics principles to solve a variety of problems.

7.4. Flexible Scheduling

We offer flexible scheduling options to fit your busy lifestyle. You can schedule tutoring sessions at times that are convenient for you, whether it’s during the day, in the evening, or on weekends.

8. Real-World Case Studies

To illustrate the importance of understanding velocity, let’s examine a few real-world case studies where accurate velocity calculations are crucial.

8.1. Case Study 1: Designing a High-Speed Train

Engineers designing high-speed trains must accurately calculate velocity to ensure safety and efficiency. They need to consider factors such as air resistance, track friction, and engine power to determine the maximum velocity the train can achieve.

Accurate velocity calculations are also essential for designing the train’s braking system. The brakes must be able to slow the train down quickly and safely, even at high speeds.

8.2. Case Study 2: Analyzing a Car Accident

Forensic investigators use velocity calculations to analyze car accidents and determine the cause. By examining skid marks, vehicle damage, and other evidence, they can estimate the velocity of the vehicles at the time of the collision.

This information can help determine who was at fault in the accident and whether any traffic laws were violated. Accurate velocity calculations are essential for ensuring justice and preventing future accidents.

8.3. Case Study 3: Launching a Rocket into Space

Launching a rocket into space requires extremely precise velocity calculations. Engineers must determine the velocity needed to escape Earth’s gravity and reach the desired orbit.

They also need to account for factors such as air resistance, engine thrust, and the mass of the rocket. Any errors in velocity calculations could result in the mission failing or the rocket going off course.

9. FAQs About Velocity

To further clarify the concept of velocity, here are some frequently asked questions:

9.1. What is the difference between velocity and acceleration?

Velocity is the rate of change of position, while acceleration is the rate of change of velocity. In other words, velocity tells you how fast an object is moving and in what direction, while acceleration tells you how quickly the velocity is changing.

9.2. Can velocity be negative?

Yes, velocity can be negative. A negative velocity indicates that the object is moving in the opposite direction to the positive direction.

9.3. What are the units of velocity?

The units of velocity are typically meters per second (m/s) or miles per hour (mph), but any unit of distance divided by a unit of time can be used.

9.4. How do you calculate average velocity?

Average velocity is calculated by dividing the total displacement by the total time taken.

9.5. What is instantaneous velocity?

Instantaneous velocity is the velocity of an object at a specific moment in time. It is the limit of the average velocity as the time interval approaches zero.

9.6. How does air resistance affect velocity?

Air resistance is a force that opposes the motion of an object through the air. It can reduce an object’s velocity, especially at high speeds.

9.7. What is relative velocity?

Relative velocity is the velocity of an object with respect to another object or frame of reference.

9.8. How can I improve my understanding of velocity?

To improve your understanding of velocity, practice solving problems, work with a tutor, and study real-world examples.

9.9. Why is understanding velocity important?

Understanding velocity is important because it is a fundamental concept in physics that has numerous practical applications in various fields, including engineering, sports, and navigation.

9.10. Where can I find expert help with velocity calculations?

At HOW.EDU.VN, we offer personalized tutoring and expert guidance to help you master velocity and other physics concepts. Contact us today to learn more.

10. Take the Next Step with HOW.EDU.VN

Understanding velocity is essential for anyone studying physics or working in a related field. At HOW.EDU.VN, we provide the resources and support you need to master this important concept.

Don’t let the complexities of velocity hold you back. Connect with our expert tutors and start building your knowledge and confidence today.

Ready to take the next step?

• Visit our website at HOW.EDU.VN to learn more about our tutoring services.
• Contact us at +1 (310) 555-1212 to schedule a consultation.
• Visit us at 456 Expertise Plaza, Consult City, CA 90210, United States.

Let HOW.EDU.VN be your guide to mastering velocity and achieving your academic and professional goals. Our team of over 100 renowned Ph.D. experts is ready to provide personalized support and answer all your questions.

Calculating Speed and Velocity

Understanding how to accurately calculate speed and velocity ensures that you can correctly measure motion in physics, incorporating both the rate of movement and its direction, which is essential for any physical analysis.

At HOW.EDU.VN, we understand that seeking expert advice is crucial for tackling complex challenges. Navigating the intricacies of physics, engineering, or any specialized field requires more than just theoretical knowledge—it demands practical solutions and personalized guidance. That’s why we’ve curated a network of over 100 world-renowned Ph.D. experts, ready to provide you with tailored insights and answers to your most pressing questions.

The Challenges You Face

Many of our clients come to us feeling overwhelmed by the complexity of their problems. They struggle with:

• Finding the right expert: Sifting through countless profiles to identify a specialist with the precise expertise needed.
• Trusting the information: Ensuring the advice they receive is credible, accurate, and up-to-date.
• Communicating effectively: Articulating their questions clearly and understanding complex answers.
• Implementing solutions: Translating expert advice into practical, actionable steps.

How HOW.EDU.VN Delivers Solutions

We bridge the gap between you and the world’s leading minds, making expert consultation accessible, reliable, and effective. Here’s how:

1. Unparalleled Expertise: Our network comprises over 100 Ph.D. experts across diverse fields, each with a proven track record of excellence.
2. Personalized Matching: We take the time to understand your specific needs and match you with the perfect expert for your unique challenge.
3. Confidential Consultations: Your privacy is our priority. We provide a secure and discreet platform for you to discuss your concerns openly.
4. Actionable Insights: Our experts deliver clear, concise, and practical advice that you can implement immediately.
5. Ongoing Support: We’re committed to your success. We offer follow-up consultations and resources to ensure you achieve your goals.

Ready to experience the power of expert guidance?

• Visit HOW.EDU.VN today to explore our network of experts.
• Contact us at +1 (310) 555-1212 for a free consultation.
• Visit us at 456 Expertise Plaza, Consult City, CA 90210, United States.

Let how.edu.vn connect you with the knowledge and support you need to overcome any obstacle and achieve your full potential.