Have you ever wondered why ice skating is possible? Gliding effortlessly across a frozen surface seems almost magical. The secret isn’t magic, but fascinating physics at play, specifically something called pressure melting and a principle described by the Clausius-Clapeyron equation. Let’s dive into the science behind how ice skates work and explore the amazing relationship between pressure, temperature, and ice.
The Slippery Secret of Ice: Pressure Melting
Ice, in its solid state, might seem like the least slippery surface. Yet, ice skating is a popular activity enjoyed by millions. The key to this seeming contradiction lies in a phenomenon known as pressure melting. Simply put, applying pressure to ice can lower its melting point, causing it to turn into water even when the temperature is below the standard freezing point of 0°C (32°F).
Think about the blade of an ice skate. It’s incredibly thin, designed to concentrate your body weight onto a very small area. This concentrated weight exerts significant pressure on the ice beneath the blade. This pressure is enough to locally melt a thin layer of ice into water. This microscopic layer of water acts as a lubricant, significantly reducing friction between the skate blade and the ice, allowing you to glide smoothly.
 Problem 15-1
Problem 15-1
The Clausius-Clapeyron Equation: The Science Behind the Slip
The scientific principle that perfectly explains pressure melting is described by the Clausius-Clapeyron equation. This equation, a cornerstone of thermodynamics, quantifies the relationship between pressure and temperature at the boundary between two phases of matter, like solid and liquid. In the case of ice skating, we’re concerned with the boundary between ice (solid) and water (liquid).
Let’s break down the Clausius-Clapeyron equation and understand how it applies to our icy scenario:
$$ frac{dP}{dT} = frac{L}{T Delta V_m} $$
Where:
- dP/dT: This represents the slope of the phase boundary line on a pressure-temperature diagram. It tells us how much the pressure changes for a small change in temperature needed to maintain equilibrium between the two phases.
- L: This is the latent heat of fusion. It’s the amount of energy (heat) required to change a substance from a solid to a liquid at a constant temperature. For ice, this is the energy needed to melt it into water.
- T: This is the absolute temperature in Kelvin.
- ΔV_m: This is the change in molar volume during the phase transition – the difference in volume between the liquid phase (water) and the solid phase (ice).
For water and ice, there’s a crucial detail: ice is less dense than water. This means that the volume of ice is greater than the volume of the same mass of water. Therefore, ΔV_m (V_water – V_ice) is a negative value.
When ΔV_m is negative, and L and T are always positive, the slope dP/dT becomes negative. This negative slope is the key! It signifies that as pressure (P) increases, the temperature (T) at which the phase transition (melting) occurs decreases. In simpler terms, increasing pressure lowers the melting point of ice.
Regelation: Ice Melting and Refreezing in Action
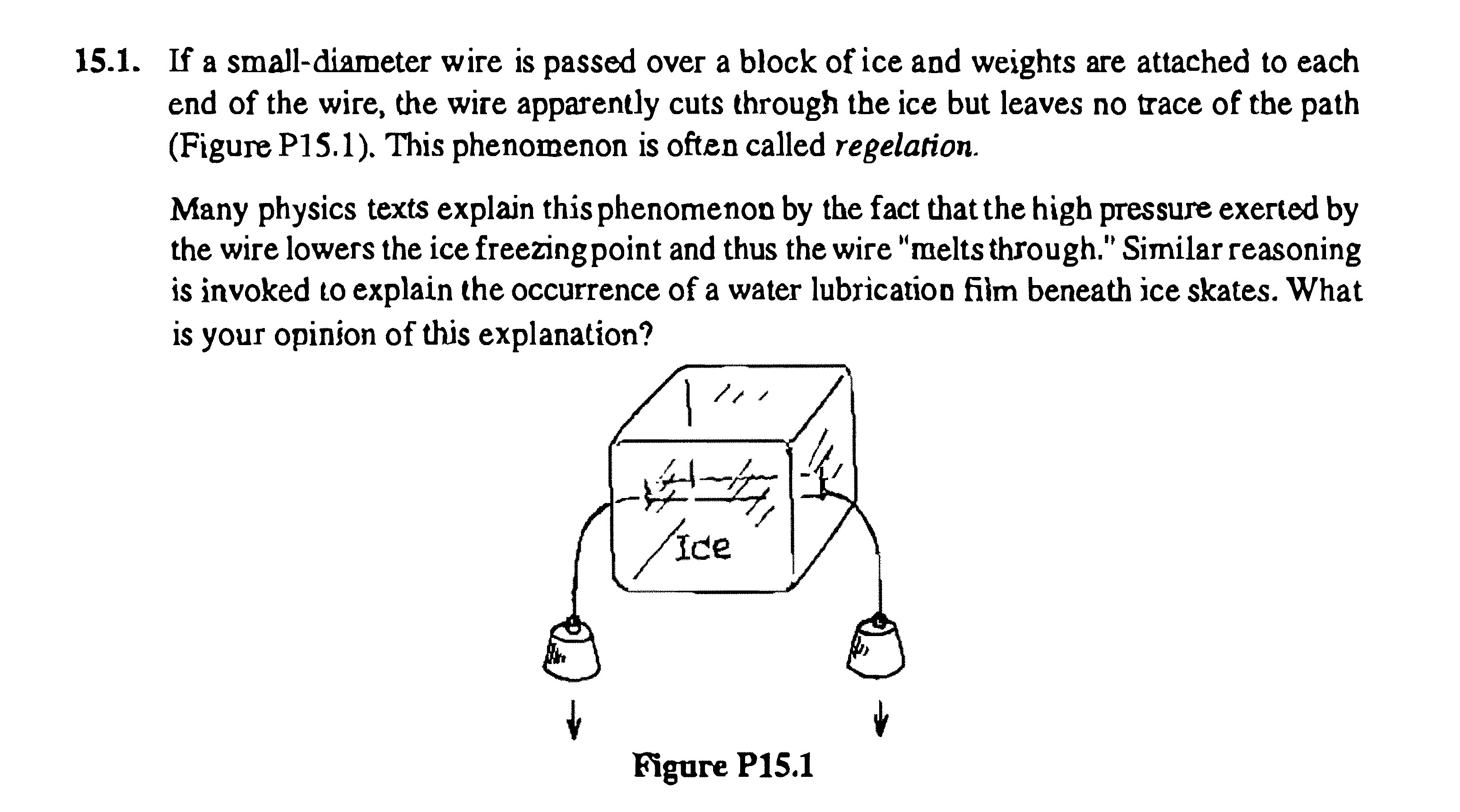
Another fascinating concept related to pressure melting and ice skating is regelation. Regelation is the process of melting under pressure and refreezing when the pressure is removed. This phenomenon is beautifully demonstrated by the classic experiment of a wire cutting through a block of ice with weights attached to each end.
The weighted wire exerts pressure on the ice directly beneath it. This pressure lowers the melting point, causing the ice under the wire to melt. The wire then moves through the melted water. As the wire passes, the pressure is released, and the water above the wire refreezes because the temperature is still below the normal freezing point. The wire effectively cuts through the ice block, but the ice block remains solid, seemingly reforming behind the wire.
This same principle of regelation contributes to the thin layer of water forming under an ice skate. The pressure from the skate blade melts the ice, creating the lubricating water layer. As the skate moves on, the pressure is removed, and the water can refreeze.
Ice Skates: Engineering for the Glide
Ice skates are ingeniously designed to maximize the effect of pressure melting. The blades are not flat; they have a hollow ground, creating two sharp edges. These edges further concentrate the skater’s weight onto an even smaller area of ice, significantly increasing the pressure. This enhanced pressure ensures that a thin layer of water is readily formed, even at moderately low temperatures, providing the essential lubrication for a smooth and enjoyable glide.
While friction does play a role in slowing a skater down, it’s the pressure-induced water layer that primarily enables the motion of ice skating. Without this fascinating interplay of pressure and phase change, ice skating as we know it wouldn’t be possible.
Conclusion
The seemingly simple act of ice skating is underpinned by complex and elegant physics. The ability to glide across ice is not due to the ice being inherently slippery, but rather due to the pressure exerted by the skate blade causing a localized melting of the ice surface. This pressure melting, scientifically explained by the Clausius-Clapeyron equation and related to the phenomenon of regelation, reveals the fascinating science hidden beneath the surface of a seemingly simple winter pastime. So, the next time you lace up your skates, remember you’re not just gliding on ice, you’re dancing with the principles of thermodynamics!
