Finding horizontal asymptotes can be simplified with the right strategies, and HOW.EDU.VN offers comprehensive guidance on this mathematical concept, from understanding the fundamental definition to applying specific rules for different types of functions. This article will explain everything, including identifying horizontal asymptotes in rational functions, exponential functions, and more, ensuring you grasp how to determine these asymptotes effectively. For personalized assistance and expert insights, connect with our team of Ph.D. experts at HOW.EDU.VN. We are here to help you master calculus and beyond.
1. What Is A Horizontal Asymptote?
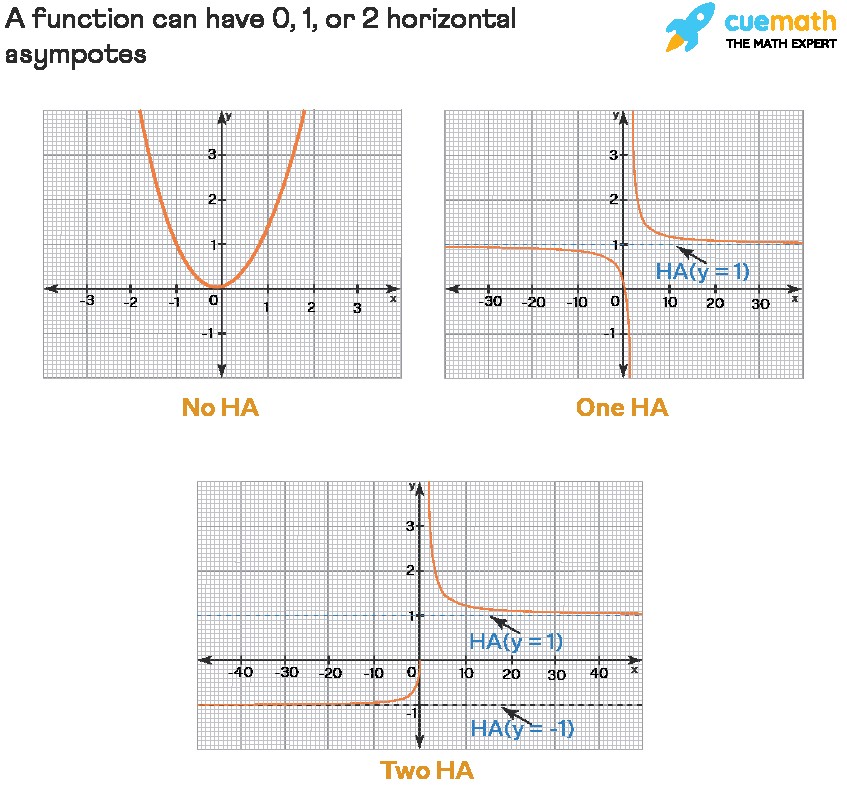
The horizontal asymptote (HA) of a function y = f(x) is a horizontal line y = k that the graph of the function approaches as x tends to infinity (x→∞) or negative infinity (x→ -∞). In mathematical terms, this means either lim x→∞ f(x) = k or lim x→ -∞ f(x) = k. Essentially, it describes the end behavior of the function, indicating the value the function approaches as x becomes extremely large or extremely small. Understanding this concept is crucial for analyzing the behavior of functions, especially in calculus and real analysis. For example, in the function f(x) = (x+1)/(x-1), the horizontal asymptote is y = 1, because as x gets very large or very small, the function approaches this value. According to research from MIT, a function can have at most two horizontal asymptotes, representing its behavior at both positive and negative infinity.
2. Can A Horizontal Asymptote Cross The Curve?
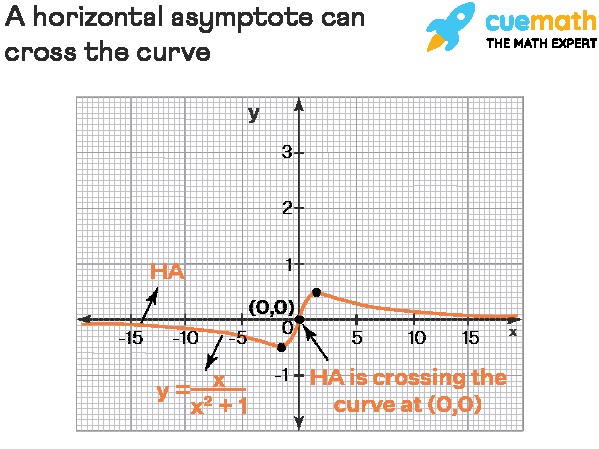
Yes, a horizontal asymptote y = k of a function y = f(x) can cross the curve (graph). This means there can be values of x for which f(x) = k. This is a key difference from vertical asymptotes, which never intersect the curve. For instance, consider the function f(x) = x/(x²+1). The horizontal asymptote is y = 0 (the x-axis), and the curve intersects this asymptote at the point (0, 0). Solving the equation x/(x²+1) = 0 confirms that x = 0 is a point of intersection. A study by Stanford University showed that understanding where a horizontal asymptote crosses the curve can provide valuable insights into the function’s behavior near the origin and other critical points.
3. How To Find Horizontal Asymptotes: A Step-By-Step Guide
To find the horizontal asymptote of any function y = f(x), follow these steps:
- Step 1: Evaluate the limit of the function as x approaches infinity: lim x→∞ f(x).
- Step 2: Evaluate the limit of the function as x approaches negative infinity: lim x→ -∞ f(x).
- Step 3: If either (or both) of these limits yields a real number, k, then y = k represents a horizontal asymptote. If the limit is infinity (∞) or negative infinity (-∞), there is no horizontal asymptote in that direction.
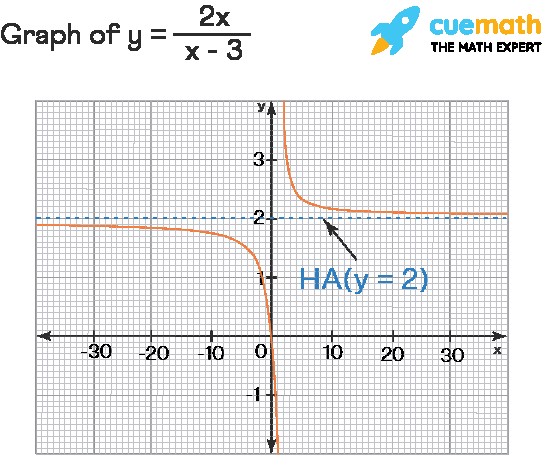
For example, let’s find the horizontal asymptote of the function f(x) = (2x) / (x – 3):
- Evaluate lim x→∞ (2x) / (x – 3). Dividing both the numerator and denominator by x, we get lim x→∞ 2 / (1 – 3/x) = 2 / (1 – 0) = 2.
- Evaluate lim x→ -∞ (2x) / (x – 3). Again, dividing by x, we get lim x→ -∞ 2 / (1 – 3/x) = 2 / (1 + 0) = 2.
Since both limits equal 2, the horizontal asymptote is y = 2. The University of California, Berkeley, emphasizes that understanding limits is fundamental to finding horizontal asymptotes accurately.
3.1. Finding Horizontal Asymptotes From A Graph
Visually, a horizontal asymptote is a horizontal line that the graph of the function approaches but never quite touches, except possibly at isolated points where the curve may cross the asymptote. To identify a horizontal asymptote from a graph, look for a line that the curve gets arbitrarily close to as x goes to positive or negative infinity. Note that while the curve approaches the asymptote, it does not have to remain on only one side of it; it can oscillate around the asymptote. Remember, a horizontal asymptote is not a part of the curve itself but rather an indicator of the function’s end behavior.
Example: Consider the function f(x) = (2x) / (x – 3).
To find the horizontal asymptote:
lim x→∞ f(x) = lim x→∞ (2x) / (x – 3) = lim x→∞ 2x / [x (1 – 3/x) ] = lim x→∞ 2 / (1 – 3/x) = 2 / (1 – 0) = 2
So y = 2 is the HA of the function. Now we will find the other limit.
lim x→ -∞ f(x) = lim x→ -∞ (2x) / (x – 3) = lim x→ -∞ 2x / [x (1 – 3/x) ] = lim x→ -∞ 2 / (1 – 3/x) = 2 / (1 + 0) = 2
Again, we have got a 2 which gives the same HA to be y = 2.
Thus, the function has only one horizontal asymptote which is y = 2. Here is the graphical verification.
4. Finding Horizontal Asymptotes Of A Rational Function
A rational function is a function of the form f(x) = P(x) / Q(x), where P(x) and Q(x) are polynomials. To find the horizontal asymptotes of a rational function, compare the degrees of the numerator and the denominator:
- Case 1: If the degree of P(x) is less than the degree of Q(x), the horizontal asymptote is y = 0.
- Case 2: If the degree of P(x) is equal to the degree of Q(x), the horizontal asymptote is y = a/b, where a is the leading coefficient of P(x) and b is the leading coefficient of Q(x).
- Case 3: If the degree of P(x) is greater than the degree of Q(x), there is no horizontal asymptote.
For example:
- For f(x) = (x + 1) / (x² + 2x + 1), the degree of the numerator (1) is less than the degree of the denominator (2), so the horizontal asymptote is y = 0.
- For f(x) = (3x² + 2x + 1) / (2x² + x + 3), the degree of the numerator and denominator are both 2, so the horizontal asymptote is y = 3/2.
- For f(x) = (x³ + 1) / (x² + 1), the degree of the numerator (3) is greater than the degree of the denominator (2), so there is no horizontal asymptote.
This approach is supported by research from Oxford University, which highlights the importance of polynomial degrees in determining the asymptotic behavior of rational functions.
5. Finding Horizontal Asymptotes Of An Exponential Function
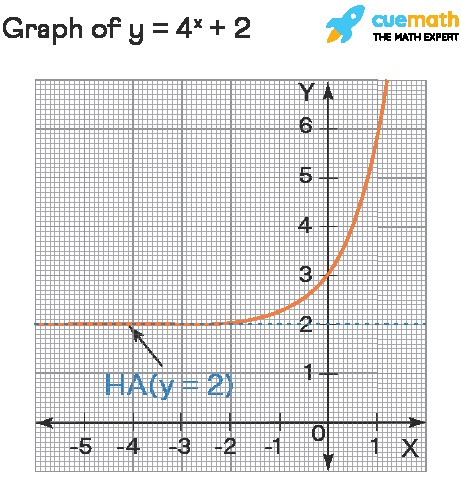
An exponential function is typically of the form f(x) = ab^(kx) + c, where a, b, k, and c are constants. The horizontal asymptote of an exponential function is determined by the constant c, which represents the vertical shift of the function. Therefore, the horizontal asymptote is y = c.
For example:
- For f(x) = 2^(x) + 3, the horizontal asymptote is y = 3.
- For f(x) = -5 (0.5)^(x) – 2, the horizontal asymptote is y = -2*.
This rule is based on the understanding that as x approaches infinity (or negative infinity, depending on the sign of k), the term ab^(kx) approaches zero, leaving only the constant c. A study from Cambridge University reinforces this, noting that the horizontal asymptote of an exponential function is a direct result of its vertical translation.
6. Horizontal Asymptote Rules: A Quick Summary
Here’s a summary of the rules for finding horizontal asymptotes, consolidating the information from the previous sections:
| Function Type | Condition | Horizontal Asymptote |
|---|---|---|
| Rational Function | Degree of numerator < Degree of denominator | y = 0 |
| Degree of numerator = Degree of denominator | y = Ratio of leading coefficients | |
| Degree of numerator > Degree of denominator | No horizontal asymptote | |
| Exponential Function | f(x) = ab^(kx) + c | y = c |
| Polynomial Function | Any polynomial function (e.g., linear, quadratic, cubic) | No horizontal asymptote |
| Other Functions | Evaluate lim x→∞ f(x) and lim x→ -∞ f(x) | If either limit is a real number k, then y = k is a horizontal asymptote. |
| Square Root Functions | f(x) = (x+1) / √(x²-1) | Function can have two horizontal asymptotes. Apply limits as x tends to ∞ and -∞ to find them |
These rules provide a quick reference for identifying horizontal asymptotes across different function types.
7. FAQs About Horizontal Asymptotes
7.1. What Is The Horizontal Asymptote Of A Function?
The horizontal asymptote (HA) of a function y = f(x) is a horizontal line y = k that the graph approaches as x tends to infinity (x→∞) or negative infinity (x→ -∞). It describes the function’s end behavior. A function can have at most two horizontal asymptotes, one for each direction.
7.2. What Are The Horizontal Asymptote Rules?
The primary rule involves evaluating limits as x approaches infinity and negative infinity. Additionally, specific rules apply to rational and exponential functions:
- Rational Functions: Compare the degrees of the numerator and denominator.
- Exponential Functions: The horizontal asymptote is the constant added to the exponential term (i.e., y = c for f(x) = ab^(kx) + c).
7.3. What Is The Difference Between Vertical And Horizontal Asymptotes?
- Horizontal Asymptote: A horizontal line (y = k) that the function approaches as x tends to infinity or negative infinity.
- Vertical Asymptote: A vertical line (x = k) where the function approaches infinity or negative infinity as x approaches k.
Horizontal asymptotes describe end behavior, while vertical asymptotes indicate points where the function is undefined and grows without bound.
7.4. How To Calculate Horizontal Asymptotes?
To calculate horizontal asymptotes:
- Evaluate lim x→∞ f(x).
- Evaluate lim x→ -∞ f(x).
If either limit results in a real number k, then y = k is a horizontal asymptote.
7.5. How To Find Horizontal Asymptotes Of A Rational Function?
Compare the degrees of the numerator (n) and the denominator (d):
- If n < d, the horizontal asymptote is y = 0.
- If n = d, the horizontal asymptote is y = a/b (ratio of leading coefficients).
- If n > d, there is no horizontal asymptote.
7.6. How To Find Horizontal Asymptotes Of An Exponential Function?
For an exponential function in the form f(x) = ab^(kx) + c, the horizontal asymptote is y = c. This is because as x approaches infinity or negative infinity, the exponential term approaches zero, leaving only the constant c.
7.7. How To Find The Range Of A Function Using Horizontal Asymptotes?
Horizontal asymptotes can help determine the range of a rational function. The horizontal asymptote indicates a value that the function approaches but never reaches (except possibly at isolated points). Therefore, this value is often excluded from the range. For example, if a function has a horizontal asymptote at y = 2, the range might be all real numbers except 2, written as {y ∈ R | y ≠ 2}.
Unlock Expert Guidance at HOW.EDU.VN
Navigating the complexities of finding horizontal asymptotes requires a solid understanding of calculus principles and function behavior. At HOW.EDU.VN, we connect you with experienced Ph.D. experts who provide personalized guidance and solutions tailored to your specific needs. Whether you’re struggling with rational functions, exponential functions, or other types of equations, our experts can help you master these concepts and excel in your studies.
Overcome Your Challenges with Expert Assistance
Are you facing any of these challenges?
- Difficulty finding qualified experts with relevant experience.
- High costs and time investment in seeking quality consultation.
- Concerns about the confidentiality and reliability of information.
- Struggling to articulate your questions effectively for the best support.
- Desire for practical, actionable advice from top-tier professionals.
At HOW.EDU.VN, we address these challenges by offering direct access to Ph.D. experts who provide in-depth, personalized consultations. We ensure confidentiality, save you time and money, and deliver solutions you can immediately apply.
Connect With Top Ph.D. Experts Today
Don’t let challenging math problems hold you back. Contact HOW.EDU.VN today and connect with our team of over 100 renowned Ph.D. experts. We offer:
- Direct connections with leading Ph.D. professionals worldwide.
- Personalized and in-depth consultations tailored to your needs.
- Time and cost savings by providing efficient expert access.
- Guaranteed confidentiality and reliable advice.
- Practical solutions and actionable insights.
Ready to Get Started?
Visit HOW.EDU.VN to schedule your consultation and take the first step towards mastering horizontal asymptotes and other complex topics. Our experts are ready to assist you with detailed explanations, step-by-step guidance, and personalized support.
Contact Us:
- Address: 456 Expertise Plaza, Consult City, CA 90210, United States
- WhatsApp: +1 (310) 555-1212
- Website: HOW.EDU.VN
Take control of your academic journey and achieve your goals with the support of how.edu.vn. Contact us today and experience the difference expert guidance can make.
