Calculus provides powerful tools for solving problems related to areas, volumes, and rates of change. One common application is finding the area of a region bounded by two curves. This technique is fundamental in various fields, from physics and engineering to economics and statistics. In this guide, we will explore a step-by-step method on How To Find The Area between two curves using definite integrals.
The concept relies on integral calculus, where the definite integral of a function over an interval represents the area under its curve and above the x-axis. When we have two functions, we can adapt this idea to find the area between them. Let’s delve into the formula and process.
Understanding the Formula for Area Between Curves
The area $A$ of the region bounded by the curves $y = f(x)$ and $y = g(x)$, and the vertical lines $x = a$ and $x = b$, where $f(x) ge g(x)$ for all $x$ in $[a, b]$, is given by the definite integral:
$A = displaystyle int_{a}^{b} [f(x) – g(x)] , dx$
Here:
- $f(x)$ represents the top curve or the upper boundary of the region.
- $g(x)$ represents the bottom curve or the lower boundary of the region.
- $a$ is the lower limit of integration, which is the x-coordinate of the leftmost intersection point or the starting x-value of the region.
- $b$ is the upper limit of integration, which is the x-coordinate of the rightmost intersection point or the ending x-value of the region.
To effectively use this formula, we need to correctly identify the top and bottom curves and determine the limits of integration. Let’s illustrate this with examples.
Step-by-Step Examples: Calculating Area Between Curves
Let’s work through a couple of examples to solidify our understanding of how to find the area between curves.
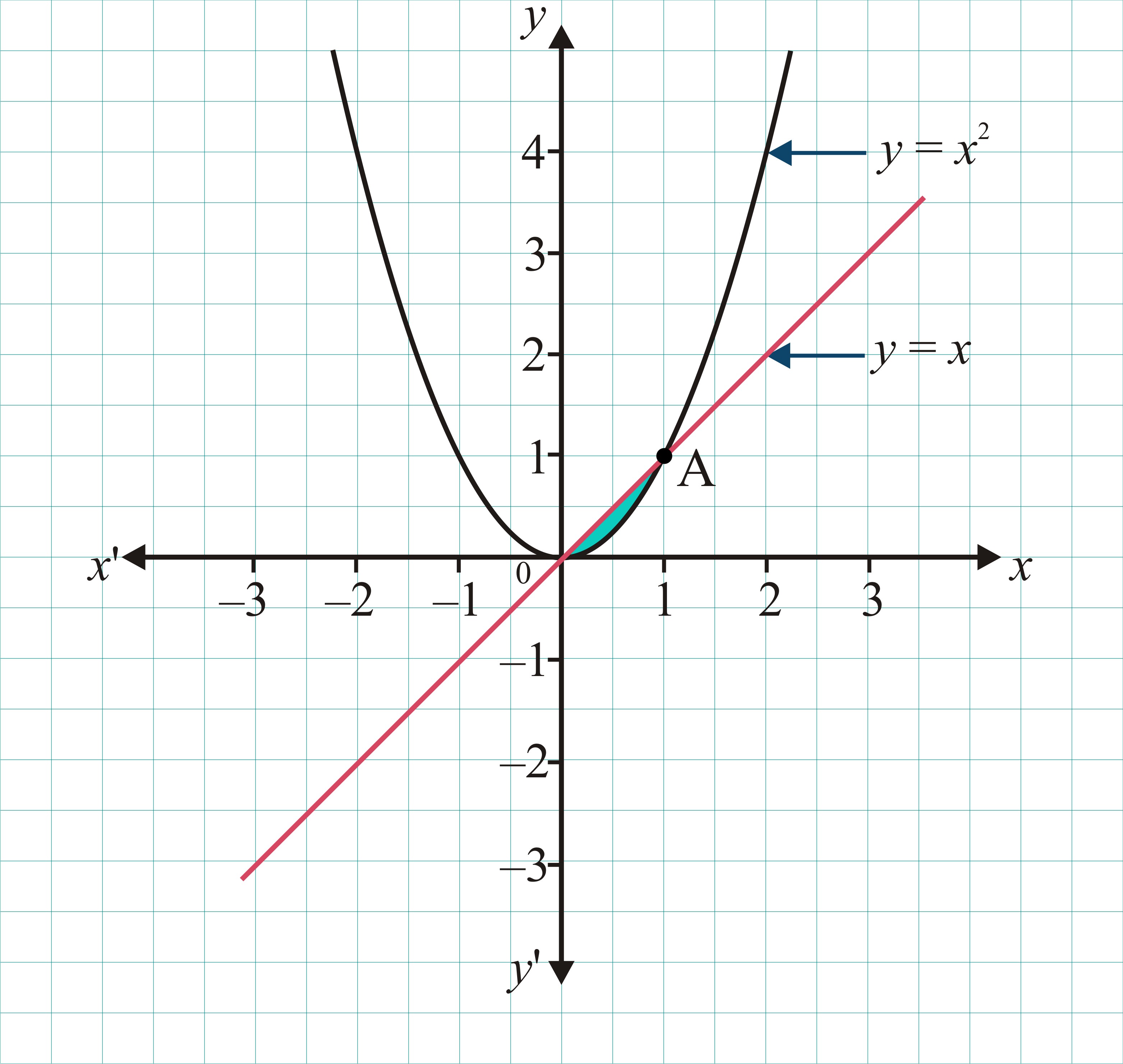
(I) Area Bounded by $y = x^2$ and $y = x$
Consider the curves $y = x^2$ and $y = x$. We want to find the area of the region enclosed by these two curves.
First, visualize the curves. $y=x$ is a straight line passing through the origin, and $y=x^2$ is a parabola opening upwards.
To find the area of the shaded region, we need to determine the limits of integration and identify the top and bottom curves within this region.
1. Identify the Top and Bottom Curves:
In the shaded region, the line $y = x$ is above the parabola $y = x^2$. Therefore, $f(x) = x$ (top curve) and $g(x) = x^2$ (bottom curve).
2. Find the Limits of Integration:
The limits of integration are the x-coordinates of the intersection points of the two curves. To find these points, set $y = x^2$ equal to $y = x$:
$x = x^2$
$x^2 – x = 0$
$x(x – 1) = 0$
This gives us $x = 0$ and $x = 1$. These are our limits of integration, so $a = 0$ and $b = 1$.
3. Set Up and Evaluate the Definite Integral:
Now, we can set up the integral to find the area:
$A = displaystyle int_{0}^{1} (x – x^2) , dx$
Evaluate the integral:
$A = left[ frac{x^2}{2} – frac{x^3}{3} right]_{0}^{1}$
$A = left( frac{1^2}{2} – frac{1^3}{3} right) – left( frac{0^2}{2} – frac{0^3}{3} right)$
$A = frac{1}{2} – frac{1}{3} = frac{3 – 2}{6} = frac{1}{6}$
Thus, the area between the curves $y = x^2$ and $y = x$ is $frac{1}{6}$ square units.
(II) Area Bounded by $y = x^2 + 1$ and $y = 2$
Let’s consider another example: finding the area bounded by the curves $y = x^2 + 1$ and $y = 2$.
Visualize the curves. $y = x^2 + 1$ is a parabola shifted one unit upwards, and $y = 2$ is a horizontal line.
1. Identify the Top and Bottom Curves:
In this case, the horizontal line $y = 2$ is above the parabola $y = x^2 + 1$ in the bounded region. So, $f(x) = 2$ and $g(x) = x^2 + 1$.
2. Find the Limits of Integration:
Find the intersection points by setting $y = x^2 + 1$ equal to $y = 2$:
$2 = x^2 + 1$
$x^2 = 1$
$x = -1, x = 1$
The limits of integration are $a = -1$ and $b = 1$.
3. Set Up and Evaluate the Definite Integral:
Set up the integral for the area:
$A = displaystyle int{-1}^{1} [2 – (x^2 + 1)] , dx$
$A = displaystyle int{-1}^{1} (1 – x^2) , dx$
Evaluate the integral:
$A = left[ x – frac{x^3}{3} right]_{-1}^{1}$
$A = left( 1 – frac{1^3}{3} right) – left( (-1) – frac{(-1)^3}{3} right)$
$A = left( 1 – frac{1}{3} right) – left( -1 + frac{1}{3} right)$
$A = 1 – frac{1}{3} + 1 – frac{1}{3} = 2 – frac{2}{3} = frac{6 – 2}{3} = frac{4}{3}$
Therefore, the area between the curves $y = x^2 + 1$ and $y = 2$ is $frac{4}{3}$ square units.
Conclusion
Finding the area between two curves is a valuable application of definite integrals. By understanding the formula, identifying the top and bottom curves, and determining the correct limits of integration, you can successfully calculate the area of various regions. This guide provides a solid foundation on how to find the area between curves, equipping you with the tools to solve a range of calculus problems.