How Do You Find the Area of a Triangle? Formulas & Examples

Are you looking for a clear guide on How To Find The Area Of A Triangle? At HOW.EDU.VN, we provide expert explanations and formulas to help you master this fundamental concept, ensuring you grasp the methods for calculating the area of any triangle, regardless of its shape or given information. Learn how to calculate triangle area with confidence and ease.

1. Understanding the Basics of Triangle Area

What exactly is the area of a triangle, and why is it important?

The area of a triangle is the measure of the two-dimensional space enclosed by its three sides. It’s a fundamental concept in geometry with applications in various fields, from architecture and engineering to computer graphics and design. Knowing how to calculate the area of a triangle is essential for solving many practical problems.

1.1 Why is Calculating Triangle Area Important?

Calculating the area of a triangle is more than just a mathematical exercise; it has real-world applications. Consider these scenarios:

• Architecture: Architects use triangle area calculations to determine the amount of material needed for triangular structures or designs.
• Engineering: Engineers apply these calculations in structural analysis, ensuring the stability and safety of bridges, buildings, and other constructions.
• Navigation: Navigators use triangles to calculate distances and positions on maps and charts.
• Computer Graphics: In computer graphics, triangle area calculations are crucial for rendering 3D models and creating realistic images.

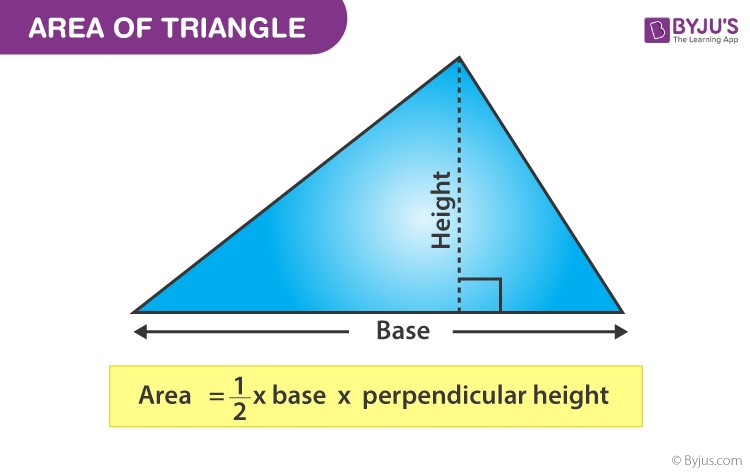
1.2 Basic Formula: Area = 1/2 Base Height

The most common formula for finding the area of a triangle is:

Area = 1/2 * base * height

Where:

• Base (b) is the length of one side of the triangle.
• Height (h) is the perpendicular distance from the base to the opposite vertex (the highest point).

This formula works for all types of triangles, but it’s essential to identify the base and corresponding height correctly. The height must form a right angle (90°) with the base.

2. Different Types of Triangles and Their Area Formulas

Triangles come in various shapes and sizes, each with its own properties. The method to find the area of a triangle can vary depending on the type of triangle you’re dealing with.

2.1 Right-Angled Triangles

A right-angled triangle (or right triangle) has one angle that measures 90°. In a right triangle, the two sides that form the right angle are called the legs, and the side opposite the right angle is called the hypotenuse.

• Formula: Area = 1/2 * base * height

  In a right triangle, the legs can be used as the base and height, making the calculation straightforward.

• Example: If a right triangle has legs of 6 cm and 8 cm, the area is 1/2 * 6 cm * 8 cm = 24 cm².

2.2 Equilateral Triangles

An equilateral triangle has all three sides equal in length and all three angles equal to 60°.

• Formula: Area = (√3 / 4) * side²

  Where “side” is the length of any of the triangle’s sides.

• Example: If an equilateral triangle has sides of 5 inches, the area is (√3 / 4) * 5² inches = (√3 / 4) * 25 inches ≈ 10.83 square inches.

2.3 Isosceles Triangles

An isosceles triangle has two sides of equal length. The angles opposite the equal sides are also equal.

• Formula: Area = (b / 4) * √(4a² - b²)

  Where “a” is the length of one of the equal sides, and “b” is the length of the base (the unequal side).

• Example: If an isosceles triangle has equal sides of 10 cm and a base of 12 cm, the area is (12 / 4) * √(4 * 10² - 12²) cm = 3 * √(400 - 144) cm = 3 * √256 cm = 3 * 16 cm = 48 cm².

2.4 Scalene Triangles

A scalene triangle has all three sides of different lengths and all three angles of different measures. To find the area of a scalene triangle when you know the lengths of all three sides, you can use Heron’s formula, as discussed in the next section.

3. Heron’s Formula: Finding Area with Three Sides

What if you only know the lengths of the three sides of a triangle? Heron’s formula is your answer. This formula is particularly useful for scalene triangles but works for all types of triangles.

3.1 Understanding Heron’s Formula

Heron’s formula allows you to calculate the area of a triangle using only the lengths of its three sides (a, b, c). The formula is:

Area = √[s(s - a)(s - b)(s - c)]

Where:

• s is the semi-perimeter of the triangle, calculated as s = (a + b + c) / 2

3.2 Steps to Apply Heron’s Formula

1. Calculate the semi-perimeter (s): Add the lengths of the three sides and divide by 2.
2. Apply Heron’s formula: Plug the value of s and the side lengths into the formula.
3. Calculate the area: Perform the calculations to find the area.

3.3 Example Using Heron’s Formula

Let’s say you have a triangle with sides a = 5 cm, b = 7 cm, and c = 10 cm.

1. Calculate s: s = (5 + 7 + 10) / 2 = 22 / 2 = 11 cm
2. Apply Heron’s formula: Area = √[11(11 - 5)(11 - 7)(11 - 10)] = √[11 * 6 * 4 * 1] = √264 ≈ 16.25 cm²

4. Using Trigonometry to Find Triangle Area

Trigonometry provides another powerful method to find the area of a triangle when you know two sides and the included angle (the angle between them).

4.1 The Sine Formula for Area

The formula for the area of a triangle using trigonometry is:

Area = 1/2 * a * b * sin(C)

Where:

• a and b are the lengths of two sides of the triangle.
• C is the angle between sides a and b.
• sin(C) is the sine of angle C.

4.2 When to Use the Sine Formula

This formula is particularly useful when you don’t know the height of the triangle but you do know two sides and the angle between them.

4.3 Example Using the Sine Formula

Suppose you have a triangle with sides a = 8 inches, b = 5 inches, and the included angle C = 60°.

1. Find the sine of the angle: sin(60°) ≈ 0.866
2. Apply the sine formula: Area = 1/2 * 8 inches * 5 inches * 0.866 = 20 * 0.866 inches ≈ 17.32 square inches

4.4 Alternative Sine Formulas

Depending on which sides and angle you know, you can use different versions of the sine formula:

• If you know sides b, c, and angle A: Area = 1/2 * b * c * sin(A)
• If you know sides a, c, and angle B: Area = 1/2 * a * c * sin(B)

5. Practical Examples and Problem Solving

Let’s walk through some practical examples to solidify your understanding of how to find the area of a triangle.

5.1 Example 1: Finding Area with Base and Height

Problem: Find the area of a triangle with a base of 10 cm and a height of 7 cm.

Solution:

• Formula: Area = 1/2 * base * height
• Plug in the values: Area = 1/2 * 10 cm * 7 cm = 35 cm²

5.2 Example 2: Using Heron’s Formula

Problem: A triangle has sides of 4 m, 13 m, and 15 m. Find its area.

Solution:

1. Calculate s: s = (4 + 13 + 15) / 2 = 32 / 2 = 16 m
2. Apply Heron’s formula: Area = √[16(16 - 4)(16 - 13)(16 - 15)] = √[16 * 12 * 3 * 1] = √576 = 24 m²

5.3 Example 3: Using Trigonometry

Problem: A triangle has sides of 9 ft and 7 ft with an included angle of 30°. Find its area.

Solution:

1. Find the sine of the angle: sin(30°) = 0.5
2. Apply the sine formula: Area = 1/2 * 9 ft * 7 ft * 0.5 = 1/2 * 63 ft * 0.5 = 15.75 ft²

6. Common Mistakes to Avoid When Calculating Triangle Area

Calculating the area of a triangle might seem straightforward, but there are some common mistakes to watch out for.

6.1 Using the Wrong Height

One of the most common errors is using a side of the triangle as the height when it’s not perpendicular to the base. Remember, the height must form a right angle with the base. If the height isn’t given, you may need to calculate it using trigonometry or other methods.

6.2 Mixing Up Units

Always ensure that the base and height are measured in the same units. If one is in centimeters and the other is in meters, convert them to the same unit before calculating the area. The area will then be in square units of that measurement (e.g., cm² or m²).

6.3 Forgetting the 1/2 Factor

The formula for the area of a triangle includes a factor of 1/2. Forgetting to include this factor will result in an area that is twice the correct value. Always double-check your calculations to ensure you’ve included the 1/2.

6.4 Incorrectly Applying Heron’s Formula

When using Heron’s formula, make sure you calculate the semi-perimeter correctly. A mistake in calculating ‘s’ will propagate through the rest of the calculation, leading to an incorrect area.

6.5 Not Using the Correct Angle with the Sine Formula

When using the sine formula (Area = 1/2 a b * sin(C)), ensure that angle C is the angle included between sides a and b. Using the wrong angle will result in an incorrect area calculation.

7. Real-World Applications of Triangle Area Calculations

The ability to find the area of a triangle has numerous practical applications across various fields. Here are a few examples:

7.1 Architecture and Construction

Architects and construction workers use triangle area calculations for various purposes, such as:

• Roofing: Calculating the area of triangular roof sections to determine the amount of roofing material needed.
• Wall Design: Designing and estimating the materials for triangular walls or facades.
• Landscaping: Determining the area of triangular plots of land for landscaping purposes.

7.2 Surveying and Mapping

Surveyors use triangle area calculations to:

• Land Measurement: Measure and divide land into triangular sections for accurate mapping.
• Area Estimation: Estimate the area of irregular plots of land by dividing them into triangles.

7.3 Engineering

Engineers use triangle area calculations in:

• Structural Analysis: Calculating the load-bearing capacity of triangular structures like trusses and bridges.
• Fluid Dynamics: Analyzing the flow of fluids around triangular objects.

7.4 Computer Graphics and Game Development

In computer graphics, triangles are the basic building blocks for creating 3D models. Triangle area calculations are used for:

• Rendering: Determining the area of each triangle on a 3D model to render it correctly.
• Collision Detection: Detecting collisions between objects by checking for overlapping triangles.

7.5 Navigation

Navigators use triangles to:

• Calculate Distances: Determine distances and positions on maps and charts using triangulation methods.
• Plot Courses: Plot courses and estimate travel times based on triangular routes.

8. Advanced Concepts and Further Learning

Once you have a solid grasp of the basic methods for finding the area of a triangle, you can delve into more advanced concepts and applications. Here are a few topics to explore:

8.1 Coordinate Geometry

If you know the coordinates of the vertices of a triangle on a coordinate plane, you can use coordinate geometry formulas to find its area. The formula involves using determinants and is particularly useful when dealing with triangles in analytical geometry.

8.2 3D Geometry

In three-dimensional space, you can find the area of a triangle using vectors. The area is half the magnitude of the cross product of two vectors formed by the sides of the triangle. This method is essential in 3D modeling and computer graphics.

8.3 Relationships to Other Geometric Shapes

Explore how the area of a triangle relates to other geometric shapes, such as parallelograms and trapezoids. Understanding these relationships can provide alternative methods for finding areas and solving complex geometric problems.

8.4 Online Resources and Courses

There are numerous online resources and courses available to further enhance your understanding of triangle area calculations and related concepts. Websites like Khan Academy, Coursera, and edX offer comprehensive lessons and practice problems.

9. Why Choose HOW.EDU.VN for Expert Guidance?

Navigating the complexities of geometry and mathematics can be challenging, but with the right guidance, it becomes much more manageable. HOW.EDU.VN offers unparalleled access to leading experts and personalized support to help you master even the most difficult concepts.

9.1 Access to Top Experts

At HOW.EDU.VN, we pride ourselves on connecting you with a network of over 100 renowned PhDs across various fields. Whether you’re struggling with triangle area calculations or need assistance with advanced mathematical concepts, our experts provide clear, accurate, and insightful guidance.

9.2 Personalized Support

We understand that every learner has unique needs and challenges. That’s why we offer personalized support tailored to your specific requirements. Our experts take the time to understand your learning style and adapt their approach to ensure you grasp the material effectively.

9.3 Comprehensive Resources

In addition to expert guidance, HOW.EDU.VN provides a wealth of comprehensive resources to support your learning journey. From detailed explanations and step-by-step examples to practice problems and real-world applications, we have everything you need to succeed.

9.4 Real-World Expertise

Our experts bring years of real-world experience to the table, providing practical insights and solutions that go beyond textbook knowledge. Whether you’re a student, professional, or lifelong learner, you can benefit from their expertise and gain a deeper understanding of the subject matter.

10. Ready to Master Triangle Area? Connect with Our Experts Today

Don’t let triangle area calculations be a source of frustration. With the right guidance and support, you can master this fundamental concept and unlock its many applications. Contact HOW.EDU.VN today and connect with our team of expert PhDs.

10.1 How HOW.EDU.VN Can Help You

• Personalized Tutoring: Receive one-on-one tutoring from experienced PhDs who can explain complex concepts in a clear and concise manner.
• Problem-Solving Assistance: Get help with specific problems or assignments and receive step-by-step solutions.
• Conceptual Understanding: Gain a deeper understanding of the underlying principles behind triangle area calculations and related concepts.
• Real-World Applications: Discover how triangle area calculations are used in various fields and industries.

10.2 Benefits of Consulting Our Experts

• Clear Explanations: Our experts can break down complex concepts into easy-to-understand terms.
• Personalized Approach: Receive tailored guidance based on your individual needs and learning style.
• Practical Insights: Benefit from real-world examples and applications that bring the material to life.
• Increased Confidence: Gain the confidence to tackle challenging problems and excel in your studies or career.

FAQ: Frequently Asked Questions on Finding the Area of a Triangle

Q1: What is the area of a triangle?

The area of a triangle is the amount of space enclosed by its three sides, measured in square units.

Q2: How do I find the area of a triangle if I know the base and height?

Use the formula: Area = 1/2 * base * height. Ensure the height is perpendicular to the base.

Q3: What if I only know the lengths of the three sides of a triangle?

Use Heron’s formula: Area = √[s(s - a)(s - b)(s - c)], where s is the semi-perimeter (s = (a + b + c) / 2).

Q4: Can I find the area of a triangle if I know two sides and the included angle?

Yes, use the formula: Area = 1/2 * a * b * sin(C), where a and b are the side lengths and C is the included angle.

Q5: What is a right-angled triangle, and how do I find its area?

A right-angled triangle has one angle of 90 degrees. Its area is found using Area = 1/2 * base * height, where the base and height are the two sides forming the right angle.

Q6: What is an equilateral triangle, and how do I calculate its area?

An equilateral triangle has all three sides equal. Its area is found using Area = (√3 / 4) * side², where “side” is the length of any side.

Q7: What is an isosceles triangle, and how do I find its area?

An isosceles triangle has two sides of equal length. Its area can be found using Area = (b / 4) * √(4a² - b²), where ‘a’ is the length of one of the equal sides, and ‘b’ is the length of the base.

Q8: What is the importance of using the correct units when calculating the area of a triangle?

Using consistent units is crucial to ensure accurate area calculation. If measurements are in different units, convert them to the same unit before applying any formula.

Q9: Where can I find reliable resources to learn more about triangle area calculations?

Reliable resources include educational websites like Khan Academy, math textbooks, and expert consultations from HOW.EDU.VN.

Q10: Why should I consult with a PhD expert at HOW.EDU.VN for help with triangle area calculations?

Consulting with a PhD expert ensures you receive accurate, personalized guidance tailored to your specific needs. Experts at HOW.EDU.VN offer clear explanations, real-world insights, and problem-solving assistance to help you master triangle area calculations.

Don’t navigate the complexities of geometry alone. Contact HOW.EDU.VN today and connect with our team of expert PhDs to master triangle area calculations and achieve your academic and professional goals.

Address: 456 Expertise Plaza, Consult City, CA 90210, United States

WhatsApp: +1 (310) 555-1212

Website: HOW.EDU.VN

Let how.edu.vn be your trusted partner in achieving mathematical excellence.