How To Find The Domain Of A Function? A Comprehensive Guide

Finding the domain of a function involves identifying all possible input values for which the function is defined, and HOW.EDU.VN offers expert guidance to navigate this crucial mathematical concept. This article will explore the methods to determine the domain of a function, providing insights suitable for students, professionals, and anyone seeking to deepen their mathematical understanding, with valuable tools for mathematical analysis and problem-solving strategies.

1. What Is The Domain Of A Function? Defining The Foundation

The domain of a function is the set of all possible input values (often denoted as ‘x’) for which the function produces a valid output. Think of it as the “ingredients” you can feed into a mathematical “machine” to get a meaningful result. As noted in 1.3 Using Function Notation, understanding domain and range is fundamental. Without a clear understanding of the domain, the function is incomplete. The domain underpins the function’s behavior, influencing the function’s behavior, graph, and applications.

2. Why Is Finding The Domain Of A Function Important? Practical Significance

Determining the domain is a crucial step when working with functions for several reasons:

Ensuring Valid Outputs: The domain ensures that the function operates on input values that produce real and meaningful outputs, avoiding undefined operations.
Understanding Function Behavior: Identifying the domain helps understand the function’s limitations and behavior, which is vital in mathematical modeling and real-world applications.
Graphing Functions Accurately: Knowing the domain allows for accurate graphing of functions, as the graph will only exist for x-values within the domain.
Solving Equations and Inequalities: Domain considerations are important when solving equations and inequalities involving functions, as solutions must fall within the domain.

3. Who Needs To Know How To Find The Domain Of A Function? Target Audience

Understanding How To Find The Domain Of A Function is essential for a diverse audience:

Students: From high school to university levels, students in mathematics, physics, engineering, and computer science need to understand domain to solve problems and grasp function concepts.
Professionals: Engineers, physicists, economists, and data scientists rely on functions in their work, requiring a solid understanding of domain to model and analyze real-world phenomena accurately.
Educators: Teachers and professors need to clearly explain the domain concept to their students, ensuring they grasp its importance and application.
Anyone Interested in Math: Individuals pursuing math as a hobby or for intellectual growth can deepen their understanding and appreciation of mathematical concepts by mastering the domain of a function.

4. When Is It Necessary To Determine The Domain? Contextual Applications

Determining the domain of a function is necessary in a variety of contexts:

Solving Mathematical Problems: When solving equations, inequalities, or systems involving functions, the domain ensures that the solutions are valid and meaningful.
Graphing Functions: When graphing functions, the domain defines the set of x-values for which the graph exists, leading to accurate and complete representations.
Modeling Real-World Scenarios: In applications such as physics, engineering, and economics, functions are used to model real-world phenomena, and the domain represents the set of valid inputs for these models.
Designing Algorithms: In computer science, when designing algorithms that use mathematical functions, the domain determines the set of inputs that the algorithm can handle correctly.

5. Where Can You Learn To Find The Domain Of A Function? Educational Resources

There are numerous resources available to learn how to find the domain of a function:

Textbooks: Mathematics textbooks covering algebra, precalculus, and calculus provide detailed explanations and examples on determining the domain of a function.
Online Courses: Platforms like Coursera, Khan Academy, and edX offer courses that cover function domains, often with video lectures, practice problems, and quizzes.
Educational Websites: Websites like Mathway, Wolfram Alpha, and Symbolab provide tools for calculating and visualizing function domains, along with explanations and examples.
Tutoring Services: Private tutoring services and academic support centers offer personalized instruction and assistance in understanding and applying function domain concepts.
HOW.EDU.VN: HOW.EDU.VN connects you with experienced Ph.D. experts who can offer personalized guidance and solutions for understanding and applying function domain concepts. Address: 456 Expertise Plaza, Consult City, CA 90210, United States. Whatsapp: +1 (310) 555-1212. Website: HOW.EDU.VN.

6. How To Express The Domain? Interval Notation Explained

The domain of a function is often expressed using interval notation, which is a way of representing a set of numbers using intervals. Key points about interval notation:

Smallest Term First: The smallest number in the interval is written first, followed by the largest number.
Parentheses and Brackets: Parentheses ( or ) indicate that the endpoint is not included (exclusive), while square brackets [ or ] indicate that the endpoint is included (inclusive).
Infinity Symbol: The infinity symbol ∞ is used to represent unbounded intervals, always with parentheses since infinity is not a specific number.

For example:

(a, b): All real numbers between a and b, not including a and b.
[a, b]: All real numbers between a and b, including a and b.
(a, ∞): All real numbers greater than a.
(-∞, b]: All real numbers less than or equal to b.

Understanding interval notation is essential for accurately representing the domain of a function.

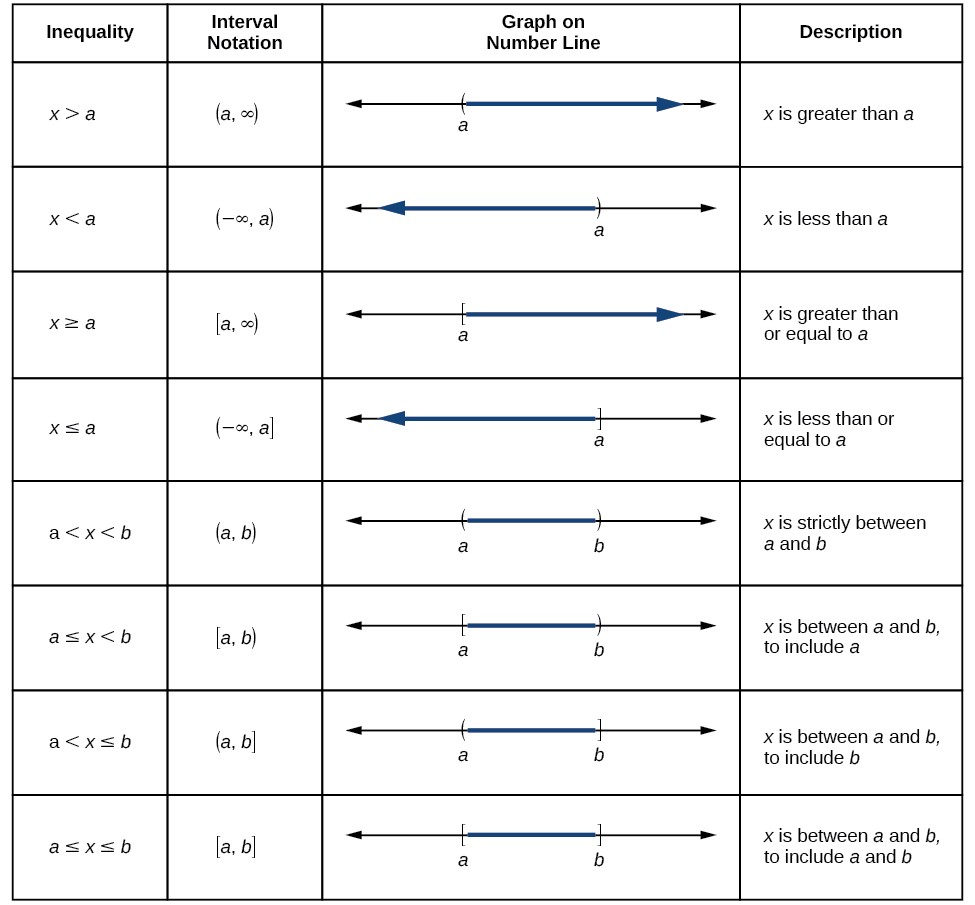Summary of interval notation.

7. Finding The Domain Of A Function: Step-by-Step Guide

Here’s a step-by-step guide to finding the domain of a function:

7.1. Identify The Input Values

Start by identifying the input variable, usually denoted as x, and consider any restrictions on its possible values.

7.2. Identify Restrictions

Determine if there are any restrictions on the input variable:

Denominators: If the function has a denominator, set the denominator equal to zero and solve for x. Exclude these values from the domain because division by zero is undefined.
Even Roots: If the function contains an even root (such as a square root), set the radicand (the expression inside the root) greater than or equal to zero and solve for x. Exclude any values that make the radicand negative.
Logarithms: If the function contains a logarithm, the argument (the expression inside the logarithm) must be greater than zero.

7.3. Write The Domain

Write the domain in interval notation, excluding any restricted values. The domain is the set of all possible input values for which the function is defined.

8. Finding Domain With Different Types Of Functions

Finding the domain varies based on the type of function. The following sections address key considerations:

8.1. Domain Of Polynomial Functions

Polynomial functions, such as linear, quadratic, and cubic functions, generally have a domain of all real numbers because there are no denominators, even roots, or logarithms.

Example: f(x) = x^2 - 1
- The domain is all real numbers, written as (-∞, ∞).

8.2. Domain Of Rational Functions

Rational functions have a denominator, so you need to exclude values that make the denominator zero.

Example: f(x) = (x + 1) / (2 - x)
1. Set the denominator equal to zero: 2 - x = 0
2. Solve for x: x = 2
3. The domain is all real numbers except x = 2, written as (-∞, 2) ∪ (2, ∞).

8.3. Domain Of Radical Functions

Functions with even roots (square root, fourth root, etc.) require the radicand to be non-negative.

Example: f(x) = √(7 - x)
1. Set the radicand greater than or equal to zero: 7 - x ≥ 0
2. Solve for x: x ≤ 7
3. The domain is all real numbers less than or equal to 7, written as (-∞, 7].

8.4. Domain Of Logarithmic Functions

Logarithmic functions require the argument (the expression inside the logarithm) to be greater than zero.

Example: f(x) = ln(x + 3)
1. Set the argument greater than zero: x + 3 > 0
2. Solve for x: x > -3
3. The domain is all real numbers greater than -3, written as (-3, ∞).

8.5. Domain Of Piecewise Functions

Piecewise functions are defined by different formulas on different intervals. The domain is the union of all intervals for which the function is defined.

Example:

f(x) = {
  x^2,   x < 0
  2x + 1,  0 ≤ x ≤ 3
  5,     x > 3
}

The domain is all real numbers, written as (-∞, ∞).

9. Real-World Examples Of Finding The Domain

Understanding the domain is vital in various real-world applications.

9.1. Physics: Projectile Motion

In physics, the height h of a projectile as a function of time t can be modeled as:

h(t) = -4.9t^2 + vt + h0

where v is the initial velocity and h0 is the initial height. The domain is t ≥ 0 because time cannot be negative.

9.2. Economics: Cost Function

In economics, the cost C of producing x items can be modeled as:

C(x) = 10x + 500

where 10x represents the variable cost and 500 represents the fixed cost. The domain is x ≥ 0 because you cannot produce a negative number of items.

9.3. Engineering: Electrical Circuits

In electrical engineering, the current I in a circuit can be modeled as:

I(t) = V / R

where V is the voltage and R is the resistance. The domain is R > 0 because resistance cannot be negative or zero.

10. Common Mistakes To Avoid When Finding The Domain

Several common mistakes can lead to incorrect domain determination:

Forgetting to Check Denominators: Always check for denominators and exclude values that make them zero.
Ignoring Even Roots: Always check for even roots and ensure the radicand is non-negative.
Neglecting Logarithms: Always check for logarithms and ensure the argument is greater than zero.
Misinterpreting Interval Notation: Use the correct notation with parentheses and brackets to indicate whether endpoints are included or excluded.
Overlooking Piecewise Functions: Consider all intervals when determining the domain of a piecewise function.
Not simplifying: Make sure that you have completely simplified the function, as well as solved for x, to be sure that you have all the appropriate values.
Assuming all real numbers: Always consider functions with even roots (square roots, fourth roots, etc.), logarithms, and rational functions.

11. Advanced Techniques For Finding The Domain

More advanced techniques can be applied to complex functions.

11.1. Composition Of Functions

For composite functions like f(g(x)), first find the domain of g(x), then ensure that the range of g(x) is within the domain of f(x).

Example: f(x) = √(x) and g(x) = 1 - x^2
1. Domain of g(x): all real numbers.
2. Range of g(x): (-∞, 1].
3. Domain of f(x): x ≥ 0.
4. Combined: 1 - x^2 ≥ 0, so -1 ≤ x ≤ 1.
5. The domain of f(g(x)) is [-1, 1].

11.2. Inverse Functions

If f(x) has an inverse function f^-1(x), the domain of f^-1(x) is the range of f(x).

Example: f(x) = e^x
1. Domain of f(x): all real numbers.
2. Range of f(x): (0, ∞).
3. Inverse function: f^-1(x) = ln(x).
4. Domain of f^-1(x): (0, ∞).

11.3. Functions With Multiple Restrictions

For functions with multiple restrictions, combine the individual restrictions to find the overall domain.

Example: f(x) = √(x - 2) / (x - 5)
1. Radicand: x - 2 ≥ 0, so x ≥ 2.
2. Denominator: x - 5 ≠ 0, so x ≠ 5.
3. The domain is [2, 5) ∪ (5, ∞).

12. How Can HOW.EDU.VN Help You Master The Domain Of A Function?

Understanding the domain of a function is crucial, and HOW.EDU.VN offers unparalleled expertise to help you master this concept. Our Ph.D. experts provide personalized guidance, addressing your specific challenges and questions. By connecting with our team, you gain access to:

Expert Insights: Learn from experienced professionals who can explain complex concepts in a clear, understandable manner.
Customized Solutions: Receive tailored advice and solutions for your unique mathematical problems.
Comprehensive Support: From basic concepts to advanced techniques, get support at every level of your mathematical journey.

13. Benefits Of Consulting Ph.D. Experts On HOW.EDU.VN

Consulting with Ph.D. experts on HOW.EDU.VN provides numerous benefits:

Accurate and Reliable Information: Receive information that is both accurate and reliable, vetted by leading experts in the field.
Personalized Learning Experience: Get a learning experience tailored to your specific needs, ensuring that you grasp the material effectively.
Time-Saving Solutions: Save time and effort by receiving direct, expert answers to your questions, avoiding the need for extensive research.
Confidence Building: Build confidence in your mathematical abilities by gaining a solid understanding of function domains and related concepts.
Improved Problem-Solving Skills: Enhance your problem-solving skills with practical tips and strategies from seasoned professionals.
Avoid Costly Errors: Working with experts can help students avoid small mistakes. These small errors can result in costly retakes or failed grades.

14. Case Studies: How Experts On HOW.EDU.VN Helped Solve Domain Problems

Here are a few case studies illustrating how experts on HOW.EDU.VN have helped individuals solve complex domain problems:

14.1. Student Struggling With Rational Functions

Challenge: A high school student was struggling with determining the domain of rational functions, particularly when the denominator had complex factors.

Solution: A Ph.D. expert on HOW.EDU.VN provided a step-by-step explanation of how to factor the denominator, identify the values that make it zero, and express the domain using interval notation. The expert also provided additional practice problems to reinforce the student’s understanding.

Outcome: The student gained confidence in finding the domain of rational functions and improved their grade in mathematics.

14.2. Engineer Modeling Physical Systems

Challenge: An engineer needed to model a physical system using a function with multiple restrictions, including square roots and logarithms.

Solution: A Ph.D. expert on HOW.EDU.VN helped the engineer identify all the restrictions, combine them correctly, and determine the valid domain for the model. The expert also provided guidance on how to interpret the domain in the context of the physical system.

Outcome: The engineer developed an accurate model of the physical system, leading to improved design and performance.

14.3. Data Scientist Analyzing Datasets

Challenge: A data scientist was analyzing a dataset with functions involving multiple compositions and inverse functions.

Solution: A Ph.D. expert on HOW.EDU.VN assisted the data scientist in breaking down the complex functions, determining the domains of individual components, and combining them to find the overall domain. The expert also provided insights into how the domain affects the interpretation of the data.

Outcome: The data scientist gained a deeper understanding of the dataset and was able to draw more meaningful conclusions.

15. Step-by-Step Guide: How To Get Help On HOW.EDU.VN

Getting help with domain of a function on HOW.EDU.VN is easy:

Visit HOW.EDU.VN: Navigate to our website.
Sign Up/Log In: Create an account or log in if you already have one.
Post Your Question: Clearly state your question or problem related to the domain of a function. Provide as much detail as possible.
Connect With An Expert: Browse the list of available Ph.D. experts and select one who specializes in mathematics and functions.
Receive Personalized Assistance: Get step-by-step guidance, explanations, and solutions tailored to your specific needs.
Address: 456 Expertise Plaza, Consult City, CA 90210, United States.
Whatsapp: +1 (310) 555-1212.
Website: HOW.EDU.VN

16. Frequently Asked Questions (FAQ) About Domain of a Function

16.1. What Is The Domain Of A Function?

The domain of a function is the set of all possible input values (x-values) for which the function produces a valid output.

16.2. Why Is Finding The Domain Important?

Finding the domain ensures that the function operates on input values that produce real and meaningful outputs, and helps to avoid undefined operations such as division by zero or taking the square root of a negative number.

16.3. How Do I Find The Domain Of A Rational Function?

For a rational function, identify any values of x that make the denominator equal to zero. Exclude these values from the domain.

16.4. What Is The Domain Of A Square Root Function?

For a square root function, ensure that the expression inside the square root (the radicand) is greater than or equal to zero. Solve for x to find the domain.

16.5. How Do I Express The Domain Using Interval Notation?

Use parentheses ( ) to indicate that an endpoint is not included and square brackets [ ] to indicate that an endpoint is included. For example, (a, b) means all numbers between a and b, not including a and b, while [a, b] means all numbers between a and b, including a and b.

16.6. Can The Domain Be All Real Numbers?

Yes, the domain can be all real numbers for some functions, such as linear and quadratic functions, where there are no restrictions on the input values.

16.7. What If A Function Has Both A Denominator And A Square Root?

In this case, you must consider both restrictions. Exclude any values that make the denominator zero and ensure that the expression inside the square root is greater than or equal to zero.

16.8. How Does The Domain Affect The Graph Of A Function?

The domain determines the set of x-values for which the graph exists. The graph will only be plotted for x-values within the domain.

16.9. What Is The Domain Of A Logarithmic Function?

For a logarithmic function, the argument (the expression inside the logarithm) must be greater than zero. Solve for x to find the domain.

16.10. Where Can I Get Help With Finding The Domain Of A Function?

You can get help from textbooks, online courses, educational websites, tutoring services, and by consulting Ph.D. experts on HOW.EDU.VN. Address: 456 Expertise Plaza, Consult City, CA 90210, United States. Whatsapp: +1 (310) 555-1212. Website: HOW.EDU.VN.

17. Call To Action: Get Expert Help With The Domain Of A Function

Don’t let challenges with the domain of a function hold you back. Whether you’re a student, professional, or math enthusiast, HOW.EDU.VN is here to provide the expert guidance you need.

Connect with our Ph.D. experts today and experience:

Personalized support tailored to your specific questions and challenges.
Clear, understandable explanations of complex concepts.
Improved problem-solving skills and confidence in your mathematical abilities.

Visit HOW.EDU.VN now and take the first step toward mastering the domain of a function. Address: 456 Expertise Plaza, Consult City, CA 90210, United States. Whatsapp: +1 (310) 555-1212. Website: how.edu.vn.