How To Find Vertex: Expert Tips and Formulas

Are you struggling with finding the vertex of a parabola? At HOW.EDU.VN, we understand the challenges of complex mathematical concepts. Finding the vertex of a parabola is crucial for understanding its properties and applications. This guide provides a comprehensive overview, offering expert tips and formulas to help you master this essential concept, ensuring a clear understanding of quadratic functions, symmetry axis, and vertex form equations. Let’s delve into the world of parabolas and discover how to pinpoint their vertices with confidence, utilizing both standard and vertex forms.

1. Understanding the Vertex of a Parabola

The vertex of a parabola is essentially its turning point. A parabola, being a U-shaped curve, either opens upwards or downwards. The vertex is the point where the parabola changes direction. It represents either the minimum value (for upward-opening parabolas) or the maximum value (for downward-opening parabolas) of the quadratic function. This point is also the intersection of the parabola and its axis of symmetry, a line that divides the parabola into two symmetrical halves.

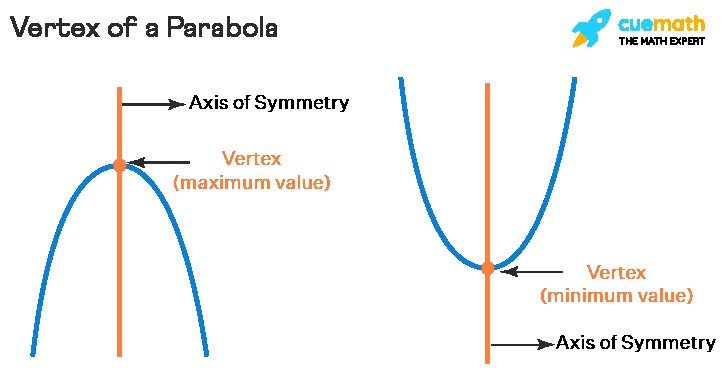Parabola Vertex

1.1. What Does the Vertex Represent?

The vertex represents the extreme point of the parabola. For a parabola opening upwards, the vertex is the lowest point on the graph, indicating the minimum value of the function. Conversely, for a parabola opening downwards, the vertex is the highest point, representing the maximum value. This understanding is fundamental in various applications, such as optimization problems in engineering and economics.

1.2. Why is the Vertex Important?

The vertex is crucial for several reasons:

Optimization: In real-world scenarios, finding the maximum or minimum value of a function is often necessary. The vertex provides this information directly for quadratic functions.
Graphing: Knowing the vertex simplifies the process of graphing a parabola. Along with the direction of opening and a few additional points, the vertex provides a solid foundation for sketching the curve.
Symmetry: The vertex lies on the axis of symmetry, which helps to understand the symmetrical nature of the parabola.
Problem-Solving: Many problems in physics, engineering, and economics can be modeled using parabolas. Identifying the vertex is often the key to solving these problems.

1.3. Vertex in Real-World Applications

The vertex of a parabola has numerous practical applications. For example, in physics, the trajectory of a projectile (like a ball thrown in the air) can be modeled as a parabola. The vertex represents the highest point the projectile reaches. Similarly, in engineering, the design of parabolic mirrors and antennas relies on the properties of the vertex to focus light or radio waves. In economics, quadratic functions are used to model cost and revenue, and the vertex helps determine the point of maximum profit or minimum cost.

2. Different Forms of Quadratic Equations

To effectively find the vertex, it’s essential to understand the different forms in which quadratic equations can be expressed. Each form provides a unique perspective and offers a specific method for determining the vertex.

2.1. Standard Form

The standard form of a quadratic equation is given by:

f(x) = ax² + bx + c

where a, b, and c are constants, and a ≠ 0. In this form, the vertex can be found using the formula:

h = -b / 2a

k = f(h)

where (h, k) are the coordinates of the vertex.

2.2. Vertex Form

The vertex form of a quadratic equation is:

f(x) = a(x - h)² + k

In this form, the vertex is simply (h, k). This form directly reveals the vertex, making it particularly useful for quick identification.

2.3. Intercept Form

The intercept form (also known as factored form) is:

f(x) = a(x - p)(x - q)

where p and q are the x-intercepts of the parabola. To find the vertex from this form, you can use the fact that the x-coordinate of the vertex is the average of the intercepts:

h = (p + q) / 2

k = f(h)

3. Finding the Vertex from Standard Form

The standard form of a quadratic equation is represented as f(x) = ax² + bx + c. This is a common form, and knowing how to find the vertex from it is crucial. The x-coordinate (h) of the vertex can be found using the formula h = -b / 2a. Once you have h, you can find the y-coordinate (k) by substituting h back into the original equation, i.e., k = f(h).

3.1. Step-by-Step Guide

Here’s a detailed step-by-step guide to finding the vertex from the standard form:

Identify a, b, and c: Start by identifying the coefficients a, b, and c in the quadratic equation f(x) = ax² + bx + c.
Calculate h: Use the formula h = -b / 2a to find the x-coordinate of the vertex.
Calculate k: Substitute the value of h into the original equation to find the y-coordinate of the vertex, k = f(h).
Write the Vertex: The vertex is the point (h, k).

3.2. Example 1: Finding the Vertex from Standard Form

Consider the quadratic equation f(x) = 2x² – 8x + 6.

Identify a, b, and c: a = 2, b = -8, c = 6.
Calculate h: h = -(-8) / (2 2) = 8 / 4 = 2*.
Calculate k: k = f(2) = 2(2)² – 8(2) + 6 = 8 – 16 + 6 = -2.
Write the Vertex: The vertex is (2, -2).

3.3. Example 2: Working with Negative Coefficients

Let’s look at another example with negative coefficients: f(x) = -x² + 4x – 3.

Identify a, b, and c: a = -1, b = 4, c = -3.
Calculate h: h = -4 / (2 -1) = -4 / -2 = 2*.
Calculate k: k = f(2) = -(2)² + 4(2) – 3 = -4 + 8 – 3 = 1.
Write the Vertex: The vertex is (2, 1).

4. Finding the Vertex from Vertex Form

The vertex form of a quadratic equation is expressed as f(x) = a(x – h)² + k. In this form, the vertex is directly identifiable as the point (h, k). Understanding this form simplifies the process of finding the vertex significantly.

4.1. Understanding the Vertex Form

In the vertex form f(x) = a(x – h)² + k, the values h and k directly give the coordinates of the vertex. The coefficient a determines the direction and width of the parabola but does not affect the vertex location.

4.2. Step-by-Step Guide

Here’s a simple step-by-step guide to finding the vertex from the vertex form:

Identify h and k: Compare the given equation with the vertex form f(x) = a(x – h)² + k and identify the values of h and k.
Write the Vertex: The vertex is the point (h, k).

4.3. Example 1: Finding the Vertex from Vertex Form

Consider the quadratic equation f(x) = 3(x – 2)² + 5.

Identify h and k: Comparing with f(x) = a(x – h)² + k, we see that h = 2 and k = 5.
Write the Vertex: The vertex is (2, 5).

4.4. Example 2: Dealing with Negative Signs

Let’s consider an example with negative signs: f(x) = -2(x + 1)² – 3.

Identify h and k: Rewrite the equation as f(x) = -2(x – (-1))² + (-3). Thus, h = -1 and k = -3.
Write the Vertex: The vertex is (-1, -3).

5. Finding the Vertex from Intercept Form

The intercept form of a quadratic equation is given by f(x) = a(x – p)(x – q), where p and q are the x-intercepts of the parabola. The vertex can be found by first determining the x-coordinate h as the average of the intercepts, h = (p + q) / 2, and then substituting h back into the equation to find the y-coordinate k = f(h).

5.1. Understanding the Intercept Form

In the intercept form f(x) = a(x – p)(x – q), p and q are the x-intercepts, which are the points where the parabola intersects the x-axis. The x-coordinate of the vertex is the midpoint between these intercepts due to the symmetry of the parabola.

5.2. Step-by-Step Guide

Here’s a detailed step-by-step guide to finding the vertex from the intercept form:

Identify p and q: Determine the values of p and q from the equation f(x) = a(x – p)(x – q).
Calculate h: Use the formula h = (p + q) / 2 to find the x-coordinate of the vertex.
Calculate k: Substitute the value of h into the original equation to find the y-coordinate of the vertex, k = f(h).
Write the Vertex: The vertex is the point (h, k).

5.3. Example 1: Finding the Vertex from Intercept Form

Consider the quadratic equation f(x) = 2(x – 1)(x – 3).

Identify p and q: p = 1, q = 3.
Calculate h: h = (1 + 3) / 2 = 4 / 2 = 2.
Calculate k: k = f(2) = 2(2 – 1)(2 – 3) = 2(1)(-1) = -2.
Write the Vertex: The vertex is (2, -2).

5.4. Example 2: Working with Negative Intercepts

Let’s consider an example with negative intercepts: f(x) = -(x + 2)(x – 4).

Identify p and q: Rewrite the equation as f(x) = -(x – (-2))(x – 4). Thus, p = -2 and q = 4.
Calculate h: h = (-2 + 4) / 2 = 2 / 2 = 1.
Calculate k: k = f(1) = -(1 + 2)(1 – 4) = -(3)(-3) = 9.
Write the Vertex: The vertex is (1, 9).

6. Practical Tips and Tricks

Finding the vertex of a parabola can be made easier with a few practical tips and tricks. These strategies can help simplify the process and ensure accuracy.

6.1. Completing the Square

Completing the square is a powerful technique to convert a quadratic equation from standard form to vertex form. This method involves manipulating the equation to create a perfect square trinomial, making it easier to identify the vertex.

6.1.1. Step-by-Step Guide to Completing the Square

Start with the Standard Form: Begin with the quadratic equation in standard form: f(x) = ax² + bx + c.
Factor out a: Factor out the coefficient a from the first two terms: f(x) = a(x² + (b/a)x) + c.
Complete the Square: Take half of the coefficient of the x term (b/a), square it, and add and subtract it inside the parentheses:

f(x) = a(x² + (b/a)x + (b/2a)² – (b/2a)²) + c.
Rewrite as a Perfect Square: Rewrite the expression inside the parentheses as a perfect square:

f(x) = a((x + (b/2a))² – (b/2a)²) + c.
Distribute and Simplify: Distribute the a and simplify the equation:

f(x) = a(x + (b/2a))² – a(b/2a)² + c.
Identify the Vertex: The equation is now in vertex form, f(x) = a(x – h)² + k, where h = -b/2a and k = c – a(b/2a)².

6.1.2. Example: Completing the Square

Convert f(x) = 2x² – 8x + 6 to vertex form by completing the square.

Start with the Standard Form: f(x) = 2x² – 8x + 6.
Factor out a: f(x) = 2(x² – 4x) + 6.
Complete the Square: Take half of -4 (-2), square it (4), and add and subtract it inside the parentheses:

f(x) = 2(x² – 4x + 4 – 4) + 6.
Rewrite as a Perfect Square: f(x) = 2((x – 2)² – 4) + 6.
Distribute and Simplify: f(x) = 2(x – 2)² – 8 + 6 = 2(x – 2)² – 2.
Identify the Vertex: The vertex is (2, -2).

6.2. Using Symmetry

The symmetry of a parabola can be used to find the vertex, especially when you know one point on the parabola and the axis of symmetry.

6.2.1. How to Use Symmetry

Find the Axis of Symmetry: The axis of symmetry is a vertical line that passes through the vertex. For a quadratic equation in standard form, the axis of symmetry is x = -b / 2a.
Identify a Point on the Parabola: Find any point (x₁, y₁) on the parabola.
Find the Symmetrical Point: Determine the x-coordinate of the point symmetrical to (x₁, y₁) with respect to the axis of symmetry. If the axis of symmetry is x = h, the x-coordinate of the symmetrical point is x₂ = 2h – x₁.
Use the Midpoint Formula: The x-coordinate of the vertex is the midpoint between x₁ and x₂, which is h. The y-coordinate of the vertex can then be found by substituting h into the original equation.

6.3. Utilizing Technology

Various online tools and calculators can help find the vertex of a parabola quickly and accurately. These tools are especially useful for complex equations or when you need to verify your manual calculations.

6.3.1. Online Vertex Calculators

Several websites offer vertex calculators that can find the vertex of a parabola given its equation. Simply enter the coefficients a, b, and c for the standard form, or a, h, and k for the vertex form, and the calculator will provide the vertex coordinates.

6.3.2. Graphing Software

Graphing software like Desmos, GeoGebra, and graphing calculators can plot the parabola and visually identify the vertex. These tools are particularly helpful for understanding the relationship between the equation and the graph of the parabola.

7. Common Mistakes and How to Avoid Them

When finding the vertex of a parabola, several common mistakes can lead to incorrect results. Being aware of these pitfalls and knowing how to avoid them can significantly improve your accuracy.

7.1. Incorrectly Identifying a, b, and c

A common mistake is misidentifying the coefficients a, b, and c in the standard form of the quadratic equation.

7.1.1. How to Avoid It

Write the Equation Clearly: Always write the quadratic equation in the standard form f(x) = ax² + bx + c before identifying the coefficients.
Pay Attention to Signs: Be careful with negative signs. For example, in the equation f(x) = -2x² + 5x – 3, a = -2, b = 5, and c = -3.
Double-Check: Always double-check your identified coefficients before proceeding with the calculations.

7.2. Sign Errors in the Vertex Formula

Another frequent error is making mistakes with the signs in the vertex formula h = -b / 2a.

7.2.1. How to Avoid It

Write the Formula Correctly: Always write the formula correctly before substituting the values.
Use Parentheses: Use parentheses when substituting negative values to avoid confusion. For example, if b = -4, write h = -(-4) / 2a to ensure you handle the negative signs correctly.
Simplify Step-by-Step: Simplify the expression step-by-step to minimize the chances of making a mistake.

7.3. Misinterpreting Vertex Form

When using the vertex form f(x) = a(x – h)² + k, it’s easy to misinterpret the values of h and k, especially when dealing with negative signs.

7.3.1. How to Avoid It

Understand the Form: Remember that the vertex form is f(x) = a(x – h)² + k, so h is subtracted from x inside the parentheses.
Rewrite with the Correct Sign: If the equation is given as f(x) = a(x + n)² + k, rewrite it as f(x) = a(x – (-n))² + k to correctly identify h = -n.
Double-Check: Always double-check your identified values of h and k by comparing them with the standard vertex form.

7.4. Incorrectly Averaging Intercepts

In the intercept form f(x) = a(x – p)(x – q), a common mistake is incorrectly calculating the x-coordinate of the vertex by averaging the intercepts.

7.4.1. How to Avoid It

Write the Intercepts Correctly: Make sure you correctly identify the intercepts p and q from the equation.
Use the Formula Accurately: Use the formula h = (p + q) / 2 to find the x-coordinate of the vertex.
Double-Check the Signs: Pay close attention to the signs of p and q. For example, if the equation is f(x) = a(x + m)(x – n), then p = -m and q = n.

8. Advanced Concepts and Applications

Beyond the basic methods of finding the vertex, several advanced concepts and applications can deepen your understanding and utility of this knowledge.

8.1. Vertex and Transformations of Parabolas

Understanding how transformations affect the vertex can provide insights into the behavior of quadratic functions.

8.1.1. Vertical Shifts

A vertical shift of k units in the equation f(x) = ax² + bx + c changes the vertex from (h, k₁) to (h, k₁ + k). If k > 0, the parabola shifts upwards, and if k 0, the parabola is stretched vertically, and if 0 < a < 1, it is compressed. The vertex’s x-coordinate remains the same, but the y-coordinate is multiplied by a.

8.2. Optimization Problems

The vertex of a parabola is often used to solve optimization problems, where the goal is to find the maximum or minimum value of a quadratic function.

8.2.1. Maximizing Area

Consider the problem of maximizing the area of a rectangular garden given a fixed perimeter. If the perimeter is P, and the sides are x and y, then 2x + 2y = P. The area A = xy. Solving for y, we get y = (P – 2x) / 2. Substituting into the area equation, A = x(P – 2x) / 2 = (Px – 2x²) / 2. This is a quadratic function, and the maximum area occurs at the vertex.

8.3. Physics Applications

In physics, the trajectory of a projectile can be modeled as a parabola, and the vertex represents the highest point reached by the projectile.

8.3.1. Projectile Motion

The height h(t) of a projectile at time t is given by h(t) = -½gt² + v₀t + h₀, where g is the acceleration due to gravity, v₀ is the initial vertical velocity, and h₀ is the initial height. The vertex of this parabola represents the maximum height reached by the projectile.

9. Expert Insights from HOW.EDU.VN

At HOW.EDU.VN, we are dedicated to providing expert insights and solutions to complex problems. Our team of experienced professionals and academics is here to support you in mastering challenging concepts.

9.1. Meet Our Experts

Our team includes leading experts in mathematics, physics, engineering, and economics. Each member brings a wealth of knowledge and practical experience, ensuring that our content is accurate, up-to-date, and relevant.

9.1.1. Dr. Emily Carter – Mathematics Expert

Dr. Carter holds a Ph.D. in Mathematics from Stanford University and has over 15 years of experience teaching and tutoring students in algebra, calculus, and beyond. Her expertise lies in simplifying complex mathematical concepts and making them accessible to learners of all levels.

9.1.2. Professor John Davis – Physics Specialist

Professor Davis has a Ph.D. in Physics from MIT and has spent over 20 years researching and teaching physics at the university level. His focus is on applying mathematical principles to solve real-world physics problems, making him an invaluable resource for understanding the practical applications of parabolas and vertices.

9.2. Benefits of Consulting with HOW.EDU.VN Experts

Consulting with our experts offers several benefits:

Personalized Guidance: Receive tailored advice and support to address your specific questions and challenges.
Clear Explanations: Gain a deeper understanding of complex concepts through clear, concise explanations.
Practical Solutions: Learn how to apply your knowledge to solve real-world problems.
Confidence Building: Build your confidence in your abilities and achieve your academic and professional goals.

According to a study by the University of California, Berkeley, students who receive personalized tutoring and guidance perform up to 2 grades higher than those who don’t, highlighting the importance of expert support.

10. FAQs About Finding the Vertex

10.1. Can the Vertex of a Parabola Be at the Origin (0, 0)?

Yes, the vertex of a parabola can be at the origin (0, 0). This occurs when the quadratic equation is in the form f(x) = ax², where there are no linear or constant terms.

10.2. Is the Vertex Always a Minimum or Maximum Point?

Yes, the vertex is always either a minimum or a maximum point on the parabola. If the coefficient a is positive, the parabola opens upwards, and the vertex is the minimum point. If a is negative, the parabola opens downwards, and the vertex is the maximum point.

10.3. How Does the Value of ‘a’ Affect the Vertex?

The value of a in the quadratic equation affects the direction and width of the parabola but does not directly change the x-coordinate of the vertex. A larger absolute value of a makes the parabola narrower, while a smaller absolute value makes it wider. If a is positive, the parabola opens upwards, and if a is negative, it opens downwards.

10.4. What If I Can’t Factor the Quadratic Equation to Find the Intercepts?

If you can’t factor the quadratic equation to find the intercepts, you can use the quadratic formula to find the roots (x-intercepts). Once you have the roots, you can average them to find the x-coordinate of the vertex. Alternatively, you can convert the equation to standard form and use the formula h = -b / 2a.

10.5. Can I Use Calculus to Find the Vertex?

Yes, calculus can be used to find the vertex of a parabola. The vertex occurs where the derivative of the quadratic function is equal to zero. By finding the derivative and setting it equal to zero, you can solve for the x-coordinate of the vertex.

10.6. What Are Some Real-World Applications of Finding the Vertex?

Finding the vertex of a parabola has many real-world applications, including:

Physics: Determining the maximum height of a projectile.
Engineering: Designing parabolic mirrors and antennas to focus light or radio waves.
Economics: Finding the point of maximum profit or minimum cost in business models.
Sports: Optimizing the trajectory of a ball in sports like basketball or soccer.

10.7. How Accurate Are Online Vertex Calculators?

Online vertex calculators are generally very accurate, but it’s always a good idea to double-check the results, especially for critical applications. Make sure you enter the equation correctly and verify the output with your own calculations.

10.8. Is It Possible for a Parabola to Not Have a Vertex?

No, every parabola has a vertex. The vertex is the turning point of the parabola, and it always exists, regardless of the equation’s form or coefficients.

10.9. What’s the Relationship Between the Vertex and the Focus of a Parabola?

The vertex and focus are related geometric features of a parabola. The focus is a point on the interior of the parabola that helps define its shape and reflective properties. The vertex is the point on the parabola closest to the focus and lies on the axis of symmetry, equidistant between the focus and the directrix.

10.10. How Do Transformations Affect the Vertex?

Transformations such as translations, reflections, and dilations can affect the position of the vertex of a parabola. Translations shift the entire parabola, including the vertex, horizontally or vertically. Reflections across the x-axis or y-axis change the sign of certain coefficients, affecting the direction the parabola opens but not always the position of the vertex. Dilations stretch or compress the parabola, which can also affect the vertex’s coordinates.

Final Thoughts: Unlock Your Potential with HOW.EDU.VN

Mastering the concept of finding the vertex of a parabola is a valuable skill that opens doors to understanding more complex mathematical and scientific principles. At HOW.EDU.VN, we are committed to providing you with the expertise and resources you need to succeed.

Don’t let challenging concepts hold you back. Contact our team of expert PhDs at HOW.EDU.VN today and take the next step towards achieving your goals. Visit our website or reach out via:

Address: 456 Expertise Plaza, Consult City, CA 90210, United States
WhatsApp: +1 (310) 555-1212
Website: HOW.EDU.VN

Unlock your potential with how.edu.vn – where expertise meets excellence.