How To Get The Area Of A Triangle? A Comprehensive Guide

Are you struggling to figure out How To Get The Area Of A Triangle? The area of a triangle represents the space enclosed within its three sides, a fundamental concept in geometry with applications across various fields. At HOW.EDU.VN, we provide expert guidance to simplify this concept and offer various methods to calculate the area of different types of triangles. Discover the simple formula, explore advanced methods, and connect with our team of expert Ph.Ds. for personalized assistance.

1. What is the Area of a Triangle?

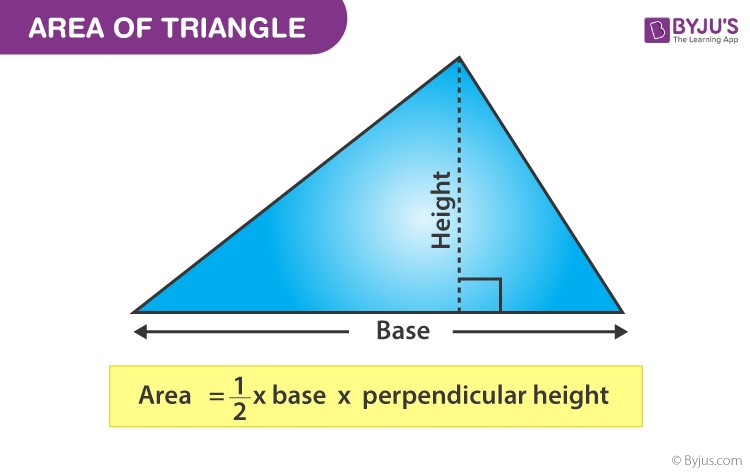
The area of a triangle is defined as the total space enclosed by its three sides. This measurement is always expressed in square units, such as square meters (m²) or square centimeters (cm²). Understanding how to calculate this area is crucial in fields ranging from architecture and engineering to everyday problem-solving. The basic formula for the area of a triangle is:

Area = 1/2 base height

This formula applies universally to all triangles, irrespective of their shape or size. It highlights that the area is directly proportional to both the base and the height of the triangle.

1.1. Why is Knowing the Area of a Triangle Important?

Knowing how to calculate the area of a triangle is more than just a mathematical exercise; it has practical implications in various real-world scenarios. Here are a few reasons why this knowledge is essential:

• Construction and Architecture: Architects and construction professionals use the area of triangles to design structures, calculate material requirements, and ensure structural stability.
• Land Surveying: Surveyors use triangular measurements to determine property boundaries, calculate land areas, and create accurate maps.
• Navigation: In navigation, the area of triangles can be used in triangulation methods to determine position and direction.
• Engineering: Engineers apply the principles of triangle area calculation in designing bridges, buildings, and other structures to ensure they can withstand various forces.
• Graphics and Design: Graphic designers and artists use triangles extensively in their designs, and knowing how to calculate their area helps in creating balanced and visually appealing compositions.

1.2. Common Challenges in Calculating Triangle Area

Despite the simplicity of the basic formula, several challenges can arise when calculating the area of a triangle:

• Identifying the Base and Height: In some triangles, especially non-right triangles, identifying the base and height can be challenging. The height must be perpendicular to the base, which may require additional calculations or constructions.
• Missing Information: Sometimes, you may not have both the base and height readily available. In such cases, you need to use other formulas or methods, such as Heron’s formula or trigonometric functions, to find the area.
• Complex Shapes: When dealing with complex shapes that can be broken down into multiple triangles, calculating the total area requires careful planning and accurate measurements to avoid errors.

2. The Fundamental Formula: Area = 1/2 Base Height

The most basic and widely used method to determine the area of a triangle involves knowing its base and height. The formula is straightforward:

Area = 1/2 base height

Where:

• base is the length of one side of the triangle.
• height is the perpendicular distance from the base to the opposite vertex.

2.1. Step-by-Step Guide to Using the Formula

Here’s a detailed guide to help you apply this formula effectively:

1. Identify the Base: Choose one side of the triangle as the base. This choice is arbitrary, but selecting a side for which you know the height can simplify the calculation.
2. Determine the Height: The height is the perpendicular distance from the base to the opposite vertex (the vertex not on the base). This might be a given value, or you may need to measure it.
3. Apply the Formula: Plug the values of the base and height into the formula: Area = 1/2 base height.
4. Calculate the Area: Perform the multiplication to find the area. Remember to include the appropriate square units (e.g., cm², m², in²).

Example: Consider a triangle with a base of 10 cm and a height of 7 cm. The area would be calculated as follows:

Area = 1/2 10 cm 7 cm = 35 cm²

2.2. Importance of Perpendicular Height

It’s crucial to remember that the height must be perpendicular to the base. This means it forms a right angle (90 degrees) with the base. If the height is not perpendicular, the formula will not yield the correct area. In non-right triangles, you might need to draw an altitude (a line from a vertex perpendicular to the opposite side) to find the height.

2.3. Practical Examples and Applications

This basic formula is widely applicable in numerous scenarios:

• Home Improvement: Calculating the amount of paint needed for a triangular wall.
• Gardening: Determining the area of a triangular flower bed.
• Crafting: Calculating the amount of fabric needed for a triangular banner.
• Construction: Estimating the area of triangular sections in building plans.

3. Area of a Right-Angled Triangle

A right-angled triangle has one angle that measures 90 degrees. In this type of triangle, calculating the area is particularly straightforward because the two sides forming the right angle can be used as the base and height.

3.1. Simplified Formula for Right Triangles

In a right triangle, if you denote the two sides forming the right angle as ‘a’ and ‘b’, the area can be calculated as:

Area = 1/2 a b

Here, one side serves as the base, and the other side serves as the height.

3.2. Calculation Example

Suppose you have a right triangle with sides a = 6 cm and b = 8 cm forming the right angle. The area is calculated as:

Area = 1/2 6 cm 8 cm = 24 cm²

3.3. Real-World Applications

• Construction: Calculating the area of cross-sections in structural designs.
• Carpentry: Determining the amount of wood needed for triangular supports.
• Engineering: Analyzing forces and stresses in right-angled triangular components.

4. Area of an Equilateral Triangle

An equilateral triangle is a special type of triangle where all three sides are of equal length, and all three angles are 60 degrees. Calculating the area of an equilateral triangle requires a specific formula that takes advantage of its unique properties.

4.1. Formula for Equilateral Triangles

If ‘s’ is the length of each side of the equilateral triangle, the area can be calculated using the formula:

Area = (√3 / 4) * s²

This formula is derived from the standard area formula (1/2 base height) and the properties of 30-60-90 right triangles formed by the altitude of the equilateral triangle.

4.2. Step-by-Step Calculation

Here’s how to use the formula:

1. Measure the Side Length: Determine the length of one side of the equilateral triangle.
2. Square the Side Length: Calculate s².
3. Multiply by √3 / 4: Multiply the result by √3 / 4 (approximately 0.433).

Example: If an equilateral triangle has a side length of 5 cm, the area would be:

Area = (√3 / 4) (5 cm)² = (√3 / 4) 25 cm² ≈ 10.825 cm²

4.3. Practical Applications

• Geometry Problems: Solving theoretical problems involving equilateral triangles.
• Design and Art: Creating patterns and designs based on equilateral triangles.
• Engineering: Analyzing symmetrical structures in mechanical designs.

5. Area of an Isosceles Triangle

An isosceles triangle has two sides of equal length. To calculate its area, you can use the standard formula (1/2 base height), but you may need to find the height first if it’s not given.

5.1. Calculating the Height

If you know the length of the two equal sides (a) and the base (b), you can calculate the height (h) using the Pythagorean theorem. The height bisects the base, forming two right triangles.

h = √(a² – (b²/4))

5.2. Area Formula for Isosceles Triangles

Once you have the height, the area can be calculated as:

Area = 1/2 b h = 1/2 b √(a² – (b²/4))

5.3. Example Calculation

Consider an isosceles triangle with equal sides of 10 cm and a base of 12 cm. First, calculate the height:

h = √(10² – (12²/4)) = √(100 – 36) = √64 = 8 cm

Now, calculate the area:

Area = 1/2 12 cm 8 cm = 48 cm²

5.4. Applications in Real Life

• Architecture: Designing roofs or facades with isosceles triangular shapes.
• Engineering: Calculating stresses in symmetrical structures.
• Construction: Cutting materials for specific triangular shapes.

6. Area of a Triangle with Three Sides (Heron’s Formula)

When you know the lengths of all three sides of a triangle but not the height, Heron’s formula is an invaluable tool. This formula allows you to calculate the area using only the side lengths.

6.1. Understanding Heron’s Formula

Heron’s formula is given by:

Area = √(s (s – a) (s – b) * (s – c))

Where:

• a, b, and c are the lengths of the three sides of the triangle.
• s is the semi-perimeter of the triangle, calculated as s = (a + b + c) / 2.

6.2. Step-by-Step Application

1. Calculate the Semi-Perimeter: Add the lengths of all three sides and divide by 2 to find ‘s’.
2. Apply Heron’s Formula: Plug the values of ‘s’, ‘a’, ‘b’, and ‘c’ into the formula.
3. Calculate the Area: Perform the calculations to find the area.

Example: Consider a triangle with sides a = 5 cm, b = 7 cm, and c = 8 cm.

1. Calculate the semi-perimeter: s = (5 + 7 + 8) / 2 = 10 cm.
2. Apply Heron’s formula:

Area = √(10 (10 – 5) (10 – 7) (10 – 8))
= √(10 5 3 2)
= √300 ≈ 17.32 cm²

6.3. Practical Uses

• Surveying: Determining land areas when only side lengths are known.
• Construction: Calculating material requirements for irregular triangular shapes.
• Navigation: Solving problems involving distances and areas in navigation.

7. Area of a Triangle Given Two Sides and the Included Angle (SAS)

When you know the lengths of two sides of a triangle and the angle between them (Side-Angle-Side or SAS), you can use a trigonometric formula to find the area.

7.1. Trigonometric Area Formula

The area of a triangle given two sides and the included angle is:

Area = 1/2 a b * sin(C)

Where:

• a and b are the lengths of the two sides.
• C is the angle between the sides a and b.
• sin(C) is the sine of angle C.

7.2. Detailed Calculation Steps

1. Identify the Sides and Angle: Determine the lengths of the two sides (a and b) and the angle (C) between them.
2. Calculate the Sine of the Angle: Find the sine of angle C using a calculator or trigonometric table.
3. Apply the Formula: Plug the values into the formula: Area = 1/2 a b * sin(C).
4. Calculate the Area: Perform the multiplication to find the area.

Example: Suppose you have a triangle with sides a = 4 cm and b = 6 cm, and the included angle C = 30 degrees.

1. Find the sine of the angle: sin(30°) = 0.5.
2. Apply the formula:

Area = 1/2 4 cm 6 cm * 0.5
= 6 cm²

7.3. Applications in Various Fields

• Navigation: Calculating distances and areas in maritime or aerial navigation.
• Engineering: Analyzing forces in structural components.
• Physics: Solving problems involving vectors and angles.

8. Advanced Methods and Techniques

Beyond the basic formulas, several advanced techniques can be used to find the area of a triangle in more complex scenarios.

8.1. Coordinate Geometry Method

If you know the coordinates of the vertices of a triangle in a coordinate plane, you can use the following formula to find the area:

Area = 1/2 * |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|

Where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the vertices.

8.2. Vector Method

Using vectors, if you have two vectors u and v forming two sides of a triangle, the area can be calculated as:

Area = 1/2 * |u x v|

Where u x v is the cross product of vectors u and v, and |u x v| is the magnitude of the cross product.

8.3. Integration Method

In calculus, if you can define the triangle’s boundaries using functions, you can find the area by integrating the function over the appropriate interval.

8.4. Software and Tools

Various software and tools can assist in calculating the area of a triangle, including:

• CAD Software: Programs like AutoCAD and SolidWorks.
• Online Calculators: Numerous websites offer triangle area calculators.
• Mathematical Software: Tools like MATLAB and Mathematica.

9. Common Mistakes to Avoid

Calculating the area of a triangle can be prone to errors if certain precautions are not taken. Here are some common mistakes to avoid:

• Using Non-Perpendicular Height: Always ensure that the height is perpendicular to the base.
• Incorrect Units: Ensure all measurements are in the same units before applying the formula.
• Misidentifying Sides: Correctly identify the sides and angles when using trigonometric formulas or Heron’s formula.
• Calculation Errors: Double-check all calculations to avoid arithmetic errors.

10. Expert Tips for Accurate Calculations

To ensure accurate calculations, consider these expert tips:

• Draw Diagrams: Always draw a diagram of the triangle to visualize the problem.
• Double-Check Measurements: Verify all measurements before plugging them into formulas.
• Use Consistent Units: Ensure all measurements are in the same units.
• Apply the Correct Formula: Choose the appropriate formula based on the given information.
• Review Your Work: Always review your calculations to catch any errors.

11. Why Choose HOW.EDU.VN for Expert Guidance?

At HOW.EDU.VN, we provide expert guidance and resources to help you master the concept of finding the area of a triangle. Our team of experienced Ph.Ds. offers personalized assistance to address your specific challenges and questions. Here’s why you should choose us:

• Expert Team: Our team consists of experienced Ph.Ds. who are experts in mathematics and related fields.
• Personalized Assistance: We offer one-on-one consultations to address your specific questions and challenges.
• Comprehensive Resources: We provide a wide range of articles, tutorials, and tools to help you understand and apply the concepts.
• Practical Solutions: We focus on providing practical solutions that you can apply in real-world scenarios.
• Trusted Guidance: We are committed to providing accurate and reliable information to help you succeed.

12. Success Stories and Testimonials

Here are some success stories from individuals who have benefited from our expert guidance:

• Architect John S.: “HOW.EDU.VN helped me understand complex calculations for triangular structures, improving my design accuracy.”
• Engineer Emily K.: “The detailed explanations and personalized support from HOW.EDU.VN were invaluable in my engineering projects.”
• Student David L.: “Thanks to HOW.EDU.VN, I aced my geometry exam with a perfect score on the triangle area problems.”

13. Consulting with Our Team of Ph.Ds.

Do you need personalized assistance with calculating the area of a triangle? Our team of expert Ph.Ds. at HOW.EDU.VN is here to help. We offer one-on-one consultations to address your specific questions and challenges.

13.1. Benefits of Consulting Our Experts

• Personalized Solutions: Receive tailored advice based on your specific needs.
• Expert Guidance: Benefit from the knowledge and experience of seasoned professionals.
• In-Depth Understanding: Gain a deeper understanding of the concepts and formulas.
• Problem-Solving Skills: Develop the skills to tackle complex problems with confidence.

13.2. How to Get Started

1. Visit Our Website: Go to HOW.EDU.VN.
2. Schedule a Consultation: Fill out the contact form to schedule a consultation with one of our experts.
3. Discuss Your Needs: During the consultation, discuss your specific challenges and questions.
4. Receive Expert Guidance: Our experts will provide personalized advice and solutions to help you succeed.

14. FAQs About Area of a Triangle

14.1. What is the area of a triangle?

The area of a triangle is the measure of the space enclosed by its three sides, typically measured in square units like square meters (m²) or square feet (ft²).

14.2. How do I calculate the area of a triangle if I know the base and height?

Use the formula: Area = 1/2 base height. Ensure the height is perpendicular to the base.

14.3. What is Heron’s formula, and when should I use it?

Heron’s formula is used when you know the lengths of all three sides of a triangle but not the height. The formula is: Area = √(s (s – a) (s – b) * (s – c)), where s is the semi-perimeter and a, b, and c are the side lengths.

14.4. How do I find the area of a right-angled triangle?

In a right-angled triangle, the two sides forming the right angle can be used as the base and height. Use the formula: Area = 1/2 a b, where a and b are the lengths of the two sides.

14.5. Can I use trigonometry to find the area of a triangle?

Yes, if you know two sides and the included angle (SAS), use the formula: Area = 1/2 a b * sin(C), where a and b are the side lengths and C is the included angle.

14.6. What if I only know the coordinates of the vertices of a triangle?

Use the coordinate geometry method: Area = 1/2 * |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|, where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the vertices.

14.7. What are some common mistakes to avoid when calculating the area of a triangle?

Common mistakes include using non-perpendicular height, incorrect units, misidentifying sides, and calculation errors.

14.8. Is there a specific formula for the area of an equilateral triangle?

Yes, the formula for the area of an equilateral triangle is: Area = (√3 / 4) * s², where s is the length of each side.

14.9. How does HOW.EDU.VN help with calculating the area of a triangle?

HOW.EDU.VN provides expert guidance, personalized assistance from experienced Ph.Ds., comprehensive resources, and practical solutions to help you master the concept.

14.10. How can I contact HOW.EDU.VN for further assistance?

You can visit our website at HOW.EDU.VN to schedule a consultation or contact us through the provided contact information.

15. Take the Next Step with HOW.EDU.VN

Don’t let the complexities of calculating triangle areas hold you back. Whether you’re a student, professional, or simply curious, HOW.EDU.VN is your go-to resource for expert guidance and personalized support.

Take the next step and unlock your full potential by connecting with our team of expert Ph.Ds. Contact us today to schedule a consultation and experience the difference that expert guidance can make.

Contact Information:

• Address: 456 Expertise Plaza, Consult City, CA 90210, United States
• WhatsApp: +1 (310) 555-1212
• Website: HOW.EDU.VN

Let how.edu.vn be your trusted partner in mastering the area of a triangle and beyond. We’re here to provide the knowledge, support, and resources you need to succeed.